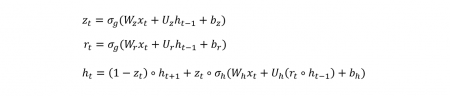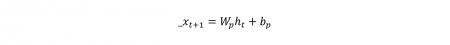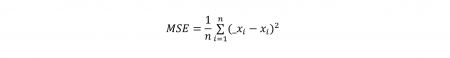Exploration de dépendances structurelles mélodiques par réseaux de neurones récurrents

Nathan Libermann, Frédéric Bimbot et Emmanuel Vincent

Résumé | Index | Plan | Texte | Bibliographie | Notes | Citation | Auteur | Version PDF | a | A

Résumés   

Index   

Index de mots-clés : réseaux de neurones récurrents, structure musicale, mélodie.

Plan   

Introduction

1La génération automatique de mélodie est une problématique régulièrement abordée en informatique musicale, mais qui reste incomplètement résolue. Récemment revenues au premier plan, les méthodes par réseaux de neurones apparaissent potentiellement capables de modéliser des mécanismes de génération de mélodie par apprentissage à partir d’exemples.

2En 2001, Chun-Chi Chen et Risto Miikkulainen furent parmi les premiers auteurs à publier sur ce sujet. L’un des principaux problèmes qu’ils relevèrent est le manque de structure globale dans les mélodies générées. D’autres auteurs, comme Judy Franklin (2005), Douglas Eck et Jürgen Schmidhuber (2002), ont alors cherché à résoudre ce problème en utilisant des réseaux récurrents long short-term memory, ou LSTM (Hochreiter et Schmidhuber, 1997), sur un corpus de musique blues ou jazz. Ces travaux ont permis d’améliorer la qualité perçue de la musique générée mais les résultats continuent à présenter une insuffisance de structure. Nicolas Boulanger-Lewandowski, Yoshua Bengio et Pascal Vincent (2012) ont tenté de combiner le modèle LSTM avec des modèles génératifs, notamment le restricted Boltzmann machines, ou RBM (Chen et Miikkulainen, 2001). Dans leur ouvrage de 2016, Allen Huang et Raymond Wu s’intéressent à la représentation des notes dans un espace vectoriel (embedding). Natasha Jaques, Shixiang Gu, Richard Turner et Douglas Eck proposent, la même année, de restreindre un modèle LSTM préalablement appris grâce à l’apprentissage par renforcement de règles de musicologie prédéfinies. L’équipe Magenta1, quant à elle, propose un modèle d’attention inspiré du travail de Dzmitry Bahdanau, Cho Kyunghyun et Bengio Yoshua (2016). À notre connaissance, il n’existe pas aujourd’hui de modèle capable d’apprendre à générer des mélodies présentant une structure pleinement satisfaisante à l’échelle de plusieurs mesures consécutives.

3Le travail présenté dans cet article est une étude exploratoire qui s’inscrit dans le cadre de la génération automatique de mélodie structurée et qui fait appel à des outils d’apprentissage profond. Nous considérons plus particulièrement le modèle séquentiel GRU (gated recurrent units ; Cho et al., 2014), que nous étudions dans différents scénarios d’apprentissage, afin de mieux comprendre les potentialités de cette approche pour la modélisation de mélodies. Nous souhaitons notamment cerner l’importance d’une hypothèse de non-ergodicité (non-invariance dans le temps) de la structure musicale, en mettant en évidence les limites des architectures récurrentes basées sur des GRU et en étudiant les possibilités de les adapter à la génération de motifs mélodiques. On suppose en effet qu’il existe une planification dans la construction d’un segment mélodique qui ne se contente pas de se référer aux k précédents éléments pour construire le suivant. Au contraire, nous faisons l’hypothèse qu’un segment mélodique forme un tout et que, au fil de ce dernier, les divers éléments se conditionnent de façon non-adjacente pour former le schéma mélodique global.

4Ainsi, dans l’esprit des travaux récents sur les modèles tensoriels/polytopiques de segments musicaux (Guichaoua, 2017 ; Louboutin et Bimbot, 2016), nous émettons l’hypothèse que, dans le cadre de mélodies simples constituées de motifs présentant des relations d’analogie, les dépendances structurelles dans la musique ne suivent pas un procédé purement séquentiel, mais plutôt des dépendances multi-échelles. Selon cette approche, un élément musical dépend de façon privilégiée des autres éléments qui se situent dans des positions métriques homologues dans le segment, plutôt que dans le voisinage immédiat. Autrement dit, les positions métriques des notes jouent un rôle dans la construction structurelle de la musique et les architectures neuronales doivent en tenir compte.

5Nous définissons donc trois modèles récurrents basés sur des GRU : un modèle à historique glissant, qui correspond à une façon « standard » de construire et d’entrainer un modèle récurrent, un modèle à historique croissant, qui correspond à une façon « dynamique » d’apprendre un modèle récurrent et enfin un modèle à historique parallèle, avec des poids distincts selon les positions à prédire.

La comparaison des différents schémas d’apprentissage proposés selon leur capacité d’encodage de l’information musicale et de leur performance de prédiction permet d’étudier la pertinence et les limites de l’hypothèse de non-ergodicité dans les séquences mélodiques.

1. Protocole expérimental

1.1. Cellule de mémoire GRU et couche de prédiction

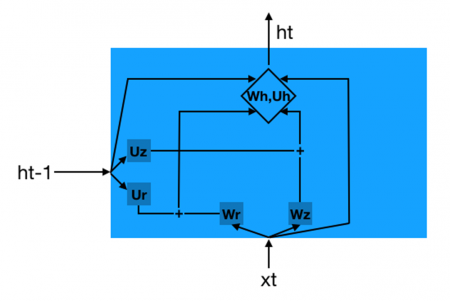
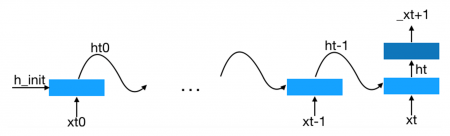
6Pour définir les architectures étudiées, nous utilisons comme unité de base le réseau de neurones récurrent GRU (voir Figure 1) qui fonctionne comme suit : à chaque instant t, la cellule GRU reçoit en entrée, sous forme de vecteurs, l’observation courante x_t et une variable interne h_t-1 qui tient lieu de mémoire des observations précédentes. À partir de ces deux entrées, la cellule GRU produit une remise à jour de h, laquelle est ensuite utilisée dans une cellule GRU semblable, qui prend h_t et l’observation x_t+1 en entrée et ainsi de suite.

Dans nos expériences, x_t est un vecteur binaire de dimensions n = 88 correspondant à un ensemble discret de notes, chaque dimension représentant une note. Ce vecteur n’a qu’un seul symbole 1 (one-hot).

La cellule GRU se décompose en six sous-ensembles de poids de propagation d’historique (U_h, U_r, U_z, W_h, W_r, W_z) qui se combinent avec les entrées h_t-1 et x_t pour former h_t selon les équations suivantes :

Où ∘ désigne le produit matriciel de Hadamard, σ_g une fonction sigmoïde et σ_h une tangente hyperbolique.

Figure 1. Gated recurrent units

Source : Nathan Libermann, 2018

7Nous avons aussi besoin, pour définir nos architectures, d’une couche de prédiction qui, à partir d’une mémoire h_t, fournit une distribution de probabilités _x_t+1 de la note suivante x_t+1. Pour ce faire, nous utilisons une couche entièrement connectée entre h_t et _x_t+1, constituée d’une matrice de poids de prédiction W_p et d’un vecteur de biais b_p, ce qui fournit en sortie une distribution de probabilité a posteriori sur l’ensemble des notes :

L’apprentissage est réalisé par rétropropagation du gradient à travers le temps (Werbos, 1990).

1.2. Spécification des architectures

8Dans cette étude, nous considérons des segments mélodiques correspondant à des unités structurelles de type phrase ou section musicale. Dans cette optique, nous modélisons des séquences de N = 64 notes, obtenues en échantillonnant des mélodies qui s’étendent sur 16 mesures.

Trois architectures basées sur des GRUs sont étudiées :

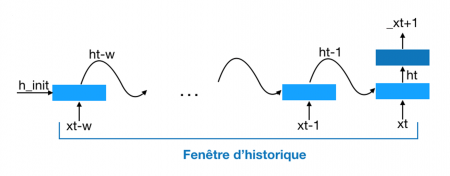
• L’architecture à historique glissant correspond à une façon standard de construire un réseau récurrent. On choisit une fenêtre d’historique de taille fixe k. Pour prédire la note _x_t+1, on alimente la couche de prédiction W_p avec l’historique h_t, qui, dans ce cas, est initialisé aléatoirement puis propagé depuis h_t-k jusqu’à h_t (voir Figure 2). La fenêtre d’historique [t - k, t] étant fixe, on ne peut calculer les prédictions _x_t+1 qu’à partir de l’instant k + 1. Les poids des couches de propagation d’historique sont partagés (c’est-à-dire indépendants de t) et il en est de même des poids des couches de prédiction. Ainsi, cette architecture repose sur une hypothèse d’invariance dans le temps des éléments musicaux.

Figure 2. Architecture à historique glissant

Source : Nathan Libermann, 2018

• L’architecture à historique croissant correspond à une façon plus dynamique de construire un modèle récurrent. Ici, on procède de la même façon que pour l’architecture du modèle à historique glissant, mais on considère une fenêtre d’historique qui couvre l’intégralité de l’intervalle [1, t] et qui, par conséquent, croît au fur et à mesure que l’on progresse dans le temps (voir Figure 3). Comme dans l’architecture précédente, les poids de la couche de propagation d’historique sont communs pour les différentes positions de notes à prédire et il en est de même pour les poids de la couche de prédiction. Dans cette variante, néanmoins, il devient possible de prédire les notes dans toutes les positions temporelles, à partir d’un historique qui va croissant. On note toutefois que cette architecture repose aussi sur une hypothèse d’invariance dans le temps, du fait du partage des poids.

Figure 3. Architecture à historique croissant

Source : Nathan Libermann, 2018

• Enfin, l’architecture à historique parallèle repose sur le même principe que l’architecture à historique croissant, à ceci près que les poids des couches de propagation et de prédiction sont indépendants pour chaque position à prédire _x_t+1. On peut ainsi voir cette configuration comme N - 1 réseaux à historique croissant, indépendants les uns des autres et correspondant à chaque position à prédire _x_t+1. L’indépendance de ces réseaux en fonction de la position est censée permettre à cette architecture de prendre en compte la non-invariance dans le temps et de tenir compte, si nécessaire, de dépendances complexes.

1.3. Données

9Pour ce travail d’exploration, nous utilisons les données du Lakh MIDI Dataset (Raffel, 2016), qui contient 176 581 fichiers MIDI multipistes sans appréciation de genres. Étant donné que nous nous intéressons uniquement aux pistes mélodiques monophoniques, nous en avons sélectionné environ 70 000 qui possédaient cette propriété dans le corpus originel. De ce sous-ensemble, nous avons extrait 8 308 blocs structurels de 16 mesures sous forme de fichier MIDI. Ne disposant pas de segmentation automatique assez fiable, nous sélectionnons uniquement les 16 premières mesures de mélodies monophoniques de type 4/4.

10Afin de permettre au modèle de pouvoir mieux extraire les relations relatives entre les notes, nous avons représenté ces mélodies en référence à la première note de la séquence (arbitrairement fixée à do), de sorte à être indépendant de la tonalité initiale. Nous obtenons donc 8 308 séquences mélodiques de 16 mesures.

11Pour simplifier la représentation traitée, on considère dans un premier temps une discrétisation de l’information mélodique dans ces segments. Nous avons procédé à un découpage des mesures en quatre portions égales et relevé à chaque fois la note active sur ces positions. Si un silence apparaît sur l’un des temps considérés, nous prolongeons la valeur de la note précédente, ce qui évite d’avoir à gérer des absences de notes.

12Le résultat de ce processus de réduction conduit à des séquences « mélodiques » de 16 mesures correspondant toutes à des successions de 64 notes. Chaque note est représentée par un vecteur de dimension 88 (correspondant aux 88 notes d’un clavier de piano). Lorsqu’une note est active, la dimension associée à cette note dans le vecteur est mise à 1 et toutes les autres à 0.

1.4. Protocole

Le corpus composé de 8 308 séquences est divisé en deux groupes A et B comprenant chacun 4 154 séquences. Nous définissons quatre scénarios pour chaque architecture (voir Table 1) :

• Apprentissage sur le groupe A, test sur le groupe A

• Apprentissage sur le groupe A, test sur le groupe B

• Apprentissage sur le groupe B, test sur le groupe A

• Apprentissage sur le groupe B, test sur le groupe B

Table 1. Protocoles d’apprentissage et de test pour mesurer les capacités de compression et de généralisation des architectures

Train	Test	Test
A	A	B
B	B	A

Source : Nathan Libermann, 2018

Lors du test, nous relevons pour chaque position de note l’erreur moyenne sur l’ensemble des exemples de test, ceci dans le cadre des trois architectures décrites dans la section 1.2.

13Les mesures effectuées en utilisant le même ensemble de test que celui utilisé pour l’apprentissage permettent de caractériser les capacités de compression de l’information mélodique par les différentes architectures, en fonction de la position de la note dans le segment musical. Celles qui croisent les ensembles d’apprentissage et de test rendent compte de la capacité de généralisation des architectures à des données nouvelles.

1.5. Critère d’évaluation

14Pour chaque instant t, nous calculons l’erreur entre le vecteur de sortie _x_t et la note réelle x_t par la fonction d’erreur quadratique moyenne (mean squared error, ou MSE). On rappelle que _x est un vecteur de dimension n = 88 correspondant à une distribution de probabilités et x un vecteur one-hot de même dimension, correspondant à la note effectivement active.

15C’est l’évolution de cette erreur que nous examinons pour chaque position de note et dans chaque scénario, afin d’observer la façon dont les différentes architectures encodent les dépendances structurelles. Nous analysons à la fois les motifs engendrés par la variation de l’erreur moyenne entre les différentes positions et le critère de compression/prédiction.

1.6. Détails complémentaires de mise en œuvre

16Pour ces expériences, nous utilisons la bibliothèque d’apprentissage profond Pytorch2. L’historique est un vecteur de dimension 100. Chaque exemple est présenté 40 fois au cours de l’apprentissage (40 epochs). L’optimiseur utilisé est Adagrad.

2. Résultats

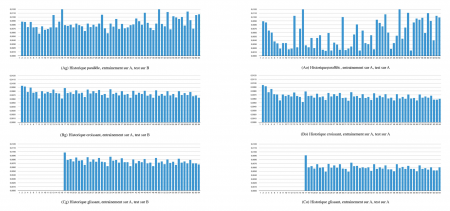
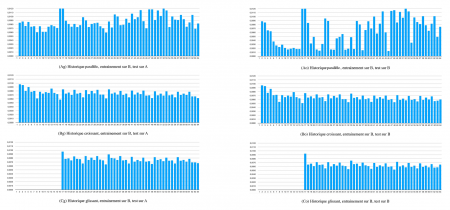
17Les figures 4 et 5 illustrent les résultats du protocole expérimental décrit dans la section précédente. La figure 4 correspond aux différentes architectures apprises à partir du corpus A et la figure 5 aux architectures apprises sur le corpus B.

Figure 4. Erreur de prédiction moyenne pour chaque position pour le corpus A

Source : Nathan Libermann, 2018

Figure 5. Erreur de prédiction moyenne pour chaque position pour le corpus B

Source : Nathan Libermann, 2018

Pour chacune de ces figures, les résultats de généralisation des architectures sont représentés sur les graphiques Ag, Bg, Cg et les résultats de compression sur les graphiques Ao, Bo et Co :

• graphique A : architecture à historique parallèle ;

• graphique B : architecture à historique croissant ;

• graphique C : architecture à historique glissant.

18En premier lieu, on constate une similarité de comportement entre courbes homologues sur la figure 4 et la figure 5. Cela permet de penser que les tendances observées sont relativement peu influencées par les spécificités des deux demi-corpus.

19On remarque ensuite que pour les architectures à historique glissant et croissant, les valeurs des capacités de généralisation (Bg et Cg) présentent un niveau d’erreur à peine plus élevé que les valeurs des capacités de compression (Bo et Co). À l’inverse, les capacités de compression et de généralisation de l’architecture parallèle se comportent très différemment l’une de l’autre. En effet, l’architecture parallèle possède beaucoup plus de paramètres libres, ce qui crée une capacité bien plus forte du réseau à comprimer les données d’apprentissage, mais entraîne un phénomène d’over-fitting (surapprentissage) qui altère la capacité de généralisation sur de nouvelle données. Ce phénomène est bien moins saillant sur les deux autres architectures.

Un examen plus précis des motifs observés sur les courbes d’erreur apporte également des observations intéressantes.

20Les courbes pour les historiques glissant et croissant présentent une pseudo-périodicité marquée à l’échelle de huit notes et des oscillations secondaires aux échelles 4 et 2, suggérant fortement une « synchronisation » des capacités de modélisation des architectures correspondantes sur des cycles de deux mesures.

21Les courbes Ao (que ce soit pour la figure 4 ou la figure 5) présentent pour leur part un comportement plus contrasté : on remarque tout d’abord une décroissance très nette sur le premier quart du segment, puis des variations plus erratiques sur la partie centrale (2^e et 3^e quart) et enfin une remontée globale de l’erreur sur le dernier quart. On peut opérer un rapprochement entre ces observations expérimentales et différentes considérations musicologiques sur la structure des segments musicaux, notamment que l’on constate souvent la réalisation de formules musicales conventionnelles en fin de segment. Ces dernières sont donc finalement moins prédictibles en fonction du contexte, puisqu’elles sont plus ou moins prédéterminées d’avance indépendamment de celui-ci.

22Par ailleurs, selon le modèle cognitif d’Implication-Réalisation d’Eugene Narmour (1990) et son extension récente par Frédéric Bimbot, Emmanuel Deruty, Gabriel Sargent et Emmanuel Vincent (2016), les fins de segments structurels constituent fréquemment des dénis d’implication par rapport aux progression musicales établies dans les portions antérieures, ce qui peut également constituer une hypothèse expliquant le comportement observé sur les courbes Ao. Toutefois, ce comportement étant moins net sur les courbes Ag, des expériences complémentaires sont requises pour mieux asseoir ces hypothèses.

Conclusions

23Dans ce travail d’exploration, nous avons considéré trois architectures de réseaux de neurones récurrents et nous avons analysé leur comportement en termes d’erreur de modélisation de schémas mélodiques simplifiés.
Ces expériences nous ont permis d’observer que la prise en compte de la non-invariance dans le temps de la structure musicale dans une architecture de réseau de neurones récurrents permet de rendre compte de façon plus fine de la structure globale des mélodies apprises par le réseau.
Dans le cadre de nos expériences actuelles, cette conclusion demeure partielle, du fait d’un volume de données d’apprentissage limité, qui entraîne une capacité insuffisante de généralisation du réseau appris.
Toutefois, cette première exploration de l’hypothèse de non-invariance dans le temps de la structure musicale, par des réseaux de neurones récurrents, nous conforte dans l’idée de poursuivre nos recherches dans cette voie.
Plusieurs pistes sont prévues pour compléter ces travaux à court terme, permettant ainsi d’enrichir ces premières investigations par des expériences supplémentaires et les résultats correspondants.

Remerciements

24Cette étude a reçu le support de l’Agence nationale de la recherche, dans le cadre du projet Dynamiques créatives de l’interaction improvisée (DYCI2, ANR-14-CE24-0002-01), et de la région Bretagne.

Bibliographie   

Notes   

Citation   

Auteur   

Quelques mots à propos de :  Nathan Libermann

Quelques mots à propos de :  Frédéric Bimbot

Quelques mots à propos de :  Emmanuel Vincent