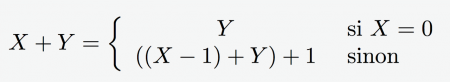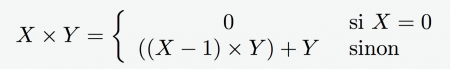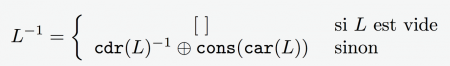Apprentissage de la programmation fonctionnelle à des étudiants en musicologie : une expérience

Philippe Ézéquel

Résumé | Index | Plan | Texte | Notes | Citation | Auteur | Version PDF | a | A

Résumés   

Index   

Index de mots-clés : machine de Peano, initiation à la programmation, programmation fonctionnelle.

Plan   

Introduction

1L’apprentissage de la programmation fonctionnelle « pure », que ce soit par des débutants en programmation ou des programmeurs plus aguerris, soulève deux problèmes pédagogiques spécifiques. Tout d’abord, la programmation fonctionnelle n’offre pas les structures de contrôle auxquelles sont habitués les programmeurs impératifs, et en particulier l’itération. Ensuite, le fait que l’itération ne soit pas disponible implique de comprendre le concept de récursivité, qui est, dans le domaine de la programmation, l’équivalent de l’induction en mathématiques.

2Ces deux difficultés sont aggravées, en ce qui concerne les débutants, par des contraintes syntaxiques ou des constructions que l’on trouve dans les langages fonctionnels traditionnels (Lisp, Scheme, Caml, etc.). Ces constructions peuvent être liées à la nécessité de disposer de dispositifs d’entrées-sortie efficaces voire agréables, comme des interfaces intuitives. Elles peuvent aussi être liées à la possibilité donnée au programmeur d’utiliser des approximations des structures de contrôles impératives classiques (permettant ainsi l’implantation d’algorithmes naturellement impératifs), ou encore à la nécessité de disposer d’outils de génie logiciel indispensables à la conception et à la maintenance de logiciels robustes, de grande taille (par exemple, des modules, une couche objet, etc.).

3La machine de Peano a été précisément conçue pour pallier ces difficultés, qui obscurcissent les notions fondamentales de la programmation pour un débutant (des outils de génie logiciel ne sont pas réellement nécessaires pour écrire des programmes de quelques lignes). Les spécifications de la machine de Peano sont une syntaxe délibérément simple, ainsi que des outils fournissant des informations pertinentes sur le programme en cours d’exécution. De plus, afin d’être en mesure d’implanter des algorithmes intéressants, les listes et les arbres binaires sont des types natifs, munis des fonctions habituelles que l’on retrouve dans d’autres langages, fonctionnels ou pas.

4L’article décrit la machine de Peano, les principes qui ont guidé sa conception, et au passage explique son nom. La syntaxe et la sémantique sont également détaillées. Son utilisation dans l’apprentissage de la programmation fonctionnelle est présentée (il s’agit du cours d’introduction à la programmation fonctionnelle du master RIM de l’UJM). Son implantation ainsi que des détails techniques sont exposés. Enfin, la conclusion évalue son utilisation non seulement dans le cadre du master RIM, mais aussi en première année de Licence d’informatique.

1. La machine de Peano

5Comme il a été dit dans l’introduction, la syntaxe de la machine de Peano doit être suffisamment simple pour être comprise non seulement par des programmeurs aguerris, mais aussi par des débutants en programmation. Cette syntaxe doit être aussi proche que possible du langage naturel, du moins en ce qui concerne la définition d’objets formels. L’objectif est qu’un non-programmeur puisse au moins suivre le déroulement d’un calcul, même s’il ne comprend pas ce qui est calculé.

6Cependant, la simplicité syntaxique ne doit pas être atteinte au prix de la puissance d’expression. La machine de Peano doit être Turing-équivalente, afin de pouvoir implanter des algorithmes intéressants, en particulier concernant les listes et les arbres.

7Dans cette section, deux versions de la machine de Peano sont présentées. Toutes les deux sont utilisées dans le cours d’introduction présenté à la section suivante. Quelle que soit la version, la machine de Peano est un évaluateur d’expressions construites à partir des opérations primitives ainsi que des fonctions définies par l’utilisateur : étant donné une expression, le résultat de l’évaluation sera un entier (positif), une liste, un arbre ou un « atome » (ces trois derniers types d’objets n’étant disponibles que dans la version dite « de luxe »).

8Pour utiliser effectivement la machine de Peano, l’utilisateur doit d’abord construire un interpréteur, en enrichissant l’interpréteur de base avec ses propres fonctions (voir la section 4 pour les détails).

1.1. Le modèle de base

9Dans sa version dite « de base », la machine de Peano comprend 5 types d’expressions :

101. (Zéro) 0 : l’évaluation de l’expression 0 donne l’entier 0 (comme prévu !).

112. (Incrémentation) ++Expr : l’évaluation de l’expression ++Expr est obtenue en ajoutant 1 au résultat de l’évaluation de l’expression Expr. Par exemple, l’évaluation de ++ ++ 0 donnera 2.

123. (Décrémentation) --Expr : l’évaluation de l’expression --Expr est obtenue en enlevant 1 au résultat de l’évaluation de l’expression Expr. Le résultat de l’évaluation de -- 0 est indéterminé.

134. (Conditionnelle) Si E₁ = E₂ alors E₃ sinon E₄ : pour évaluer cette conditionnelle, la machine de Peano commence par évaluer les expressions E₁ et E₂. Si les résultats de ces évaluations sont égaux, alors le résultat de l’évaluation de la conditionnelle est celui de l’évaluation de l’expression E₃. Si les résultats de ces évaluations sont différents, alors le résultat de l’évaluation de la conditionnelle est celui de l’évaluation de l’expression E₄.

145. (Appel de fonction) f(E₁,...,E_n) : f est une fonction définie par l’utilisateur. La machine de Peano commence par évaluer les expressions E₁,...,E_n, puis utilise le résultat de ces évaluations comme arguments, dans cet ordre, de la fonction f.

15Par exemple, en supposant définie une fonction binaire mult multipliant ses arguments (cette fonction est présentée à la section suivante), la factorielle d’un entier est calculée par la fonction suivante :

fact(N) = si N = 0 alors ++ 0

              sinon mult(N, fact(--N))

16conformément à la définition par récurrence de la factorielle :

0 ! = 1

n ! = n.(n-1) !

17Le nom de machine de Peano vient des opérations primitives de ce modèle de base. En effet, Giuseppe Peano, mathématicien italien de la fin du xix^e et du début du xx^e siècle, a donné une axiomatisation des entiers naturels utilisant entre autres 0, la fonction successeur (qui est l’incrémentation de la machine de Peano) et le principe d’induction (qui peut être obtenu en utilisant la conditionnelle et l’appel de fonctions).

18En dépit de sa simplicité, la machine de Peano est Turing-équivalente. En fait, elle comprend les fonctions récursives primitives de base :

191. 0 : c’est l’expression 0.

202. successeur : c’est l’incrémentation.

213. projections : par exemple, la seconde projection d’un triplet est réalisée par la fonction :

second(X,Y,Z) = Y

22La machine de Peano permet aussi de définir de nouvelles fonctions par composition, récursion et minimisation :

231. composition : par exemple, la composition de la fonction binaire h avec les deux fonctions unaires g₁ et g₂ est définie par

f(X) = h(g₁(X), g₂(X))

242. récursion : par exemple, la récursion de la fonction ternaire h avec la fonction unaire gest définie par :

f(X, Y) = si X = 0 alors g(Y)

                  sinon h(X, f(--X, Y), Y)

253. minimisation : par exemple, si h est une fonction binaire, la minimisation de h est obtenue à l’aide des deux fonctions f et g suivantes :

f(X) = g(X,0)

g(X,Y) = si h(X, Y) = 0 alors Y

       sinon g(X, ++Y)

26Ainsi la machine de Peano permet de construire toutes les fonctions récursives, et donc, par le théorème de Kleene, elle est Turing-équivalente.

1.2. Le modèle de luxe

27La simplicité du modèle de base de la machine de Peano est un atout quand il s’agit d’introduire la récursivité par le biais de la programmation de fonctions simples dont les algorithmes sont connus de (presque) tous. Cependant, au fur et à mesure que les algorithmes deviennent plus complexes, cette simplicité devient gênante : non seulement l’intérêt des étudiants faiblit, mais aussi cette simplicité même est un boulet. D’abord, les fichiers à compiler doivent inclure toutes les fonctions nécessaires, ce qui induit un accroissement significatif de leur taille et donc du temps de compilation. Mais surtout, ce qui est plus important, il se pose un problème de complexité : par exemple, l’algorithme pour l’addition présenté à la section suivante est de complexité exponentielle en fonction de la taille de ses arguments.

28De plus, comme mentionné dans l’introduction, la machine de Peano doit proposer les fonctionnalités présentes dans les langages fonctionnels réels (Lisp, Scheme, Caml, etc.). Il est donc nécessaire d’inclure les types de données dont ces langages disposent, à savoir les listes et les arbres.

29Le modèle de base est donc étendu en ajoutant les fonctionnalités suivantes :

301. Les opérations arithmétiques usuelles, en notation infixe habituelle. Ces opérations sont l’addition (+), la soustraction (-), la multiplication (*), le quotient (/) et le reste (%).

312. Les comparaisons usuelles, notées comme dans les autres langages de programmation.

323. Le type Liste, dont les opérateurs sont dénotés par les mêmes noms qu’en Lisp ou Scheme, avec la même sémantique (cons, car, cdr, vide). Les listes sont notées comme en Prolog, commençant par [, suivi par une suite éventuellement vide d’éléments séparés par des virgules, finissant par ]. Par exemple, [4, 6, 9, 5] dénote la liste dont le car est 4 et dont le cdr est [6, 9, 5]. Les éléments d’une liste peuvent être des entiers, des listes, des arbres ou des atomes.

334. Le type Arbre, avec les opérateurs :

• consarbre(R,G,D) qui renvoie l’arbre de racine R, de sous-arbre gauche G et de sous-arbre droit D ;

• gauche(A) (resp. droite(A)) qui renvoie le sous-arbre gauche (resp. droit) de l’arbre binaire non vide A ;

• racine(A) qui renvoie la racine de l’arbre binaire non vide A ;

• vide(A)qui renvoie 1 si A est l’arbre vide et 0 sinon.

34Les racines des arbres peuvent être des entiers, des listes, des arbres ou des atomes. L’arbre obtenu par l’appel consarbre(R,G,D) est représenté par {R, G, D}. L’arbre vide est représenté par {}.

355. Les atomes sont simplement des identifiants précédés par la quote ‘. Ils sont leur propre valeur. Par exemple, l’atome ‘toto a pour valeur ‘toto.

36Avec ces nouvelles fonctionnalités, il devient possible d’implanter tous les algorithmes classiques sur les listes et les arbres. Elles ouvrent aussi la voie à des exercices non triviaux (par exemple, représentation d’une expression arithmétique, dérivation d’une telle expression, simplification de l’expression obtenue).

2. Un exemple de parcours pédagogique

37Cette section détaille le parcours pédagogique qui a été utilisé depuis plusieurs années dans le master RIM de l’UJM.

38La machine de Peano étant disponible en deux modèles, le cours d’introduction à la programmation fonctionnelle est lui aussi découpé en deux parties.

39D’abord, le modèle de base est utilisé pour programmer des algorithmes simples et bien connus sur les entiers. L’intérêt de cette étape est double : tout d’abord elle sert à introduire puis à familiariser les étudiants avec le concept de récursivité ; puis elle montre, sur des exemples spécifiques, qu’il y a deux sortes de récursivité, la récursivité pure et la récursivité « itérative », utilisant des accumulateurs.

40Ensuite, une fois le concept de récursivité (plus ou moins) maîtrisé, le type abstrait Liste est introduit. En tant que type récursif, il permet de programmer des exercices standards faisant appel aux compétences en programmation récursive acquises à l’étape précédente. Cette deuxième partie est l’occasion de mettre l’accent sur trois aspects de l’activité de programmation, indépendamment du paradigme utilisé (impératif, fonctionnel, logique) :

1. Divers algorithmes, de complexités tout aussi diverses, peuvent résoudre le même problème ;

2. Les choix de programmation influent sur la complexité pratique des programmes ;

3. Comme le dit R. O’Keefe, « l’élégance n’est pas optionnelle ».

2.1. Le difficile apprentissage de la récursivité

41Cette étape est constituée d’une suite de problèmes que les étudiants doivent résoudre. Le premier d’entre eux consiste à programmer l’addition de deux entiers : il faut écrire la fonction plus(X,Y) qui renvoie la somme des deux entiers X et Y. L’intérêt de cette fonction est qu’elle peut être programmée de façon purement récursive, ou bien itérativement, en utilisant un accumulateur, les deux versions étant de même complexité.

42La version purement récursive utilise la définition classique de l’addition, proposée par Giuseppe Peano, qui est donnée aux étudiants :

43Cette définition est (presque) immédiatement traduite en la fonction :

         plus(X, Y) = si X = 0 alors Y sinon ++plus(--X, Y)

44Ce premier exercice comporte deux difficultés pédagogiques. La première est liée au fait que, habituellement, l’appel récursif semble magique aux étudiants, jusqu’à ce qu’ils réalisent qu’un appel récursif n’est pas autre chose que l’utilisation d’une hypothèse d’induction implicite. Le mode Trace de la machine de Peano, décrit à la section 4, permet de lever l’ambiguïté à ce sujet. La seconde difficulté pédagogique provient de la surcharge du symbole + dans la définition formelle. En effet, la première occurrence est l’appel récursif, et la seconde dénote l’incrément.

45Une fois que cette première version de l’addition est comprise, une autre version est proposée, plus procédurale : pour additionner X à Y, il suffit d’incrémenter Y X fois. Il faut donc compter le nombre de fois que Y est incrémenté, et il y a deux façons de faire ceci : l’une où l’on décrémente X jusqu’à ce qu’il atteigne 0, l’autre où l’on utilise un accumulateur, initialisé à 0, incrémenté en même temps que Y, jusqu’à ce qu’il atteigne X.

46La première version itérative est très proche dans sa forme de la version purement récursive :

     plus2(X, Y) = si X = 0 alors Y sinon plus2(--X, ++Y)

47La proximité n’est pas fortuite, elle résulte de ce que les deux fonctions implantent le même algorithme, puisque l’incrémentation et l’appel récursif peuvent permuter. Il s’agit là d’un exemple instructif de deux implantations différentes d’un même algorithme.

48La seconde version itérative utilise un accumulateur qui compte le nombre d’incrémentations de Y. Si l’algorithme est bien compris des étudiants, son implantation nécessite l’utilisation d’une fonction auxiliaire, récursive terminale, qui est la traduction d’une itération et dont les arguments sont les variables apparaissant dans la boucle. On a donc les définitions suivantes :

      plus3(X, Y) = plus3_aux(X, Y, 0)

      plus3_aux(X, Y, Z) = si X = Z alors Y

                   sinon plus3_aux(X, ++Y, ++Z)

49Malgré l’utilisation d’une variable apparemment inutile (le troisième argument de plus3_aux), plus3 est particulièrement intéressante puisqu’elle montre qu’on peut se passer de la décrémentation pour additionner. L’exercice suivant consiste alors à programmer la décrémentation, en utilisant les quatre autres primitives, c’est-à-dire à programmer la fonction decr(X) qui renvoie X - 1, et dont le résultat est indéterminé si X = 0. L’expérience montre que peu d’étudiants trouvent un algorithme par leurs propres moyens, même parmi les programmeurs chevronnés, alors qu’il s’agit d’une procédure éminemment impérative. Il suffit d’avoir deux compteurs, l’un initialisé à 0 et l’autre à 1 ; on les incrémente simultanément, jusqu’à ce que celui initialisé à 1 atteigne X. À ce moment-là, l’autre compteur contient X - 1. On a donc les définitions suivantes (il faut utiliser, une fois encore, une fonction auxiliaire représentant l’itération) :

      decr(X) = decr_aux(X, 0, 1)

      decr_aux(X, Y, Z) = si X = Z alors Y

                         sinon decr_aux(X, ++Y, ++Z)

50Cet exercice met en relief un nouveau point didactique, en montrant ce qu’« indéterminé » signifie. Dans cet exemple, l’appel decr(0) mène à une suite infinie d’appels récursifs, ce que l’on nomme « boucle » dans le jargon impératif.

51Si peu d’étudiants trouvent l’algorithme pour décrémenter, encore plus rares sont ceux qui réalisent qu’en fait, plus3_aux et decr_aux sont une seule et même fonction, comme on peut le constater en comparant leurs codes. En fait, une simple récurrence montre que :

        decr_aux(X, Y, Z) = X + Y – Z

52et, incidemment, X + Y - Z est un invariant de la boucle dénotée par la fonction decr_aux.

53Les participants sont alors invités à consolider les compétences acquises à ce point, en écrivant les fonctions suivantes, dans cet ordre, puisque par exemple la soustraction et les comparaisons sont nécessaires pour calculer le quotient et le reste :

541. moins(X, Y) qui renvoie X - Y (si X < Y le résultat est indéterminé). Il est intéressant de noter que très peu d’étudiants pensent à réutiliser la fonction decr_aux, puisque, évidemment :

moins(X, Y) = decr_aux(X, 0, Y)

55Ils préfèrent adopter l’approche utilisée pour l’addition, c’est-à-dire poser une définition formelle de la soustraction, qui est ensuite implantée soit de façon purement récursive, soit de façon itérative.

562. mult(X, Y) qui renvoie le produit X x Y. La seule différence avec l’addition est la valeur du cas de base et l’utilisation de l’addition au lieu de l’incrémentation dans l’appel récursif, conformément à la définition

57Ici aussi, il est possible d’implanter mult de deux façons, par récursivité pure ou par itération, en utilisant des accumulateurs.

583. inf(X, Y)qui renvoie 1 si X <= Y, et 0 sinon. La difficulté de l’exercice est la découverte de l’algorithme. Dans la version récursive pure, il faut décrémenter Y jusqu’à ce qu’il atteigne X ou 0. Dans la version itérative, on initialise un compteur à 0 et on l’incrémente jusqu’à ce qu’il atteigne X ou Y. Dans les deux cas, la première valeur atteinte permet de décider. Une fois l’algorithme trouvé, la programmation procède comme pour decr_aux.

594. reste(X, Y) qui renvoie le reste de la division euclidienne de X par Y. La programmation de l’algorithme (soustraire Y à X jusqu’à ce qu’une valeur strictement plus petite que Y soit atteinte) est, à ce stade, une pure formalité.

605. quotient(X, Y) qui renvoie le quotient de la division euclidienne de X par Y. La différence avec l’exercice précédent est que l’on doit compter combien de fois il faut soustraire Y à X pour atteindre le reste. Ceci se programme purement récursivement, ou itérativement, avec un compteur (et donc une fonction auxiliaire).

2.2. Vers Lisp… et au-delà !

61La machine de Peano n’est pas seulement une introduction à la récursivité, elle est aussi conçue comme une introduction à la programmation en Lisp. À cet égard, il est nécessaire de pouvoir manipuler des listes. Cette partie du cours commence avec la présentation du modèle de luxe de la machine de Peano, ainsi que la définition formelle des listes : une liste1 est :

62- soit la liste vide [ ]

63- soit obtenue en consant, dans cet ordre, un entier et une liste.

64Il est indiqué aux étudiants que cette définition récursive implique que les algorithmes sur les listes seront naturellement récursifs. Deux catégories de fonctions sur les listes sont alors définies, dont les noms proviennent du jargon de la programmation orientée objet :

65- les observateurs : ces fonctions prennent une ou plusieurs listes en argument, et renvoient une information sur la ou les listes. Par exemple, la fonction renvoyant le nombre d’éléments d’une liste (ou bien, de façon équivalente, sa longueur), ou bien une fonction comparant deux listes, ou bien une fonction renvoyant un élément remarquable d’une liste (le premier, le dernier, le N-ième, le plus petit…) sont toutes des observateurs :

66- les constructeurs : ces fonctions construisent et renvoient une liste. Par exemple, la concaténation de deux listes (le fait de placer une liste à la suite d’une autre), le renversement d’une liste (la liste obtenue en plaçant les éléments dans l’ordre inverse), et ainsi de suite.

67Dans les deux cas, un principe heuristique de programmation est présenté :

68- pour écrire un observateur, il faut caractériser le cas de base (souvent la liste vide) et déterminer le résultat dans ce cas. Ensuite, on doit déterminer ce que la fonction doit renvoyer dans le cas d’une liste de carX et de cdrL. Par exemple, pour l’observateur donnant le nombre d’éléments d’une liste :

69• le cas de base est la liste vide [] qui comporte 0 élément, valeur à retourner ;

70• le nombre d’éléments de la liste cons(X, L) est 1 (il s’agit de X), plus le nombre d’éléments de L, obtenu par un appel récursif.

71- Pour écrire un constructeur, il faut aussi caractériser le ou les cas de base, et quoi retourner dans ces cas. Ensuite il faut déterminer ce que doit être la liste à retourner, en répondant aux deux questions :

72Ainsi qu’il a été mentionné au début de la section, les listes permettent à l’enseignant de mettre l’accent sur trois points importants en programmation :

1. l’implantation a une influence sur la complexité pratique ;

2. il existe différents algorithmes de différentes complexités pour un même problème ;

3. l’élégance n’est pas optionnelle.

2.2.1. Implantation efficace d’un algorithme

73Afin de montrer aux étudiants que l’implantation d’un algorithme a de profondes répercussions sur la complexité pratique d’un programme, le problème de trouver le plus petit élément d’une liste non vide est présenté. Les étudiants, appliquant l’heuristique présentée ci-dessus, arrivent assez facilement à l’algorithme suivant : soit L une liste non vide ;

• si L a un seul élément, c’est le minimum ;

• si L a plus d’un élément, le minimum de L est le plus petit entre car(L) et le minimum de cdr(L), ce dernier étant obtenu par un appel récursif.

74La programmation de cet algorithme implique deux difficultés :

1. Comment savoir si une liste possède un seul élément ?

2. Comment utiliser le résultat de l’appel récursif ?

75Concernant la première question, l’idée la plus fréquemment trouvée par les étudiants est de calculer la longueur de la liste, avec la fonction longueur que l’on vient de définir. Très rares sont les étudiants qui réalisent qu’une liste à un seul élément possède un cdr vide, et que ceci peut être testé en deux opérations primitives, vide(cdr(L)). D’un autre côté, l’appel longueur(L) est de complexité linéaire en la longueur de L ; au total on aura donc une complexité (au moins) quadratique pour la fonction minimum, puisque la longueur de l’argument est calculée à chaque appel récursif.

76En ce qui concerne la seconde question, les étudiants écrivent toujours le fragment de code suivant :

si car(L) < minimum(cdr(L)) alors car(L) sinon minimum cdr(L)

77Rechercher le plus petit élément d’une liste devient alors impraticable dès lors que la liste possède plus de quelques éléments, puisque, en utilisant le code ci-dessus, la fonction est de complexité exponentielle : l’expression minimum(cdr(L)) est évalué 2 fois par appel récursif. Pour obtenir une complexité linéaire, on doit factoriser le fragment de code en écrivant une nouvelle fonction. La fonction minimum s’écrit donc finalement :

     minimum(L) = si vide(cdr(L)) alors car(L)

                           sinon min(car(L), minimum(cdr(L)))

     

     min(X, Y) = si X < Y alors X sinon Y

78Dans le cours de programmation Lisp, qui suit cette introduction à la programmation fonctionnelle, cette fonction donne un bon exemple de l’intérêt de la construction let, présente dans la plupart sinon tous les langages fonctionnels (Lisp, Scheme, Caml, etc.)

2.2.2. Complexité d’un algorithme

79La notion de complexité d’un algorithme (et non celle de la fonction implantant un algorithme) est illustrée par le problème de renverser une liste2. La définition formelle du renversement est donnée aux étudiants en dénotant  la concaténation de listes :

80À partir de cette définition, les étudiants arrivent assez facilement à écrire une fonction de renversement pour la machine de Peano. La fonction suivante est alors présentée :

     myst(L, M) = si vide(L) alors M

                         sinon myst(cdr(L), cons(car(L), M))

81Invités à trouver ce que renvoie cette fonction, les étudiants arrivent, par essais et erreur, à la conclusion que

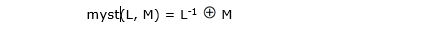
82à partir de quoi ils trouvent facilement une autre version du renversement :

     renverser(L) = myst(L, [])

83Des tests empiriques, menés à l’aide de la fonctionnalité calc de la machine de Peano (cf. section 4), semblent montrer que la version du renversement utilisant myst est plus efficace que celle dérivant de la définition formelle du renversement (en fait, cette dernière est de complexité quadratique alors que l’autre est de complexité linéaire). Une nouvelle fonction est alors présentée :

     toto(L) = si vide(L) alors L

                   sinon si vide(cdr(L)) alors L

                   sinon cons(car(toto(cdr(L))),

                                    toto(cons(car(L),

                                           toto(cdr(toto(cdr(L)))))))

84Interrogés sur ce que cette fonction peut bien renvoyer, les étudiants arrivent, péniblement et plus ou moins formellement, à la conclusion que la fonction toto renverse son argument. Des tests empiriques sont réalisés pour comparer objectivement les trois versions du renversement. Les étudiants réalisent alors que la fonction toto est inutilisable dès que l’argument a plus de quelques éléments (en fait toto est de complexité exponentielle en la longueur de son argument, même en factorisant les deux appels récursifs toto(cdr(L))).

2.2.3. Élégance et programmation

85Pour finir avec la programmation fonctionnelle, et pour montrer que l’élégance n’est pas optionnelle, les étudiants sont invités à écrire 2 fonctions :

861. somme_rangs_pairs(L) qui renvoie la somme des éléments de rang pair de la liste L,

872. somme_rangs_impairs(L) qui renvoie la somme des éléments de rang impair de la liste L, le car de la liste ayant le rang 1.

88Après beaucoup d’efforts, de nombreuses solutions, même pas fausses, sont proposées. Il est remarquable qu’en vingt ans d’enseignement, un seul étudiant ait proposé la solution la plus élégante :

    

   somme_rangs_pairs(L) = si vide(L) alors 0

                              sinon somme_rangs_impairs(cdr(L))

   somme_rangs_impairs(L) = si vide(L) alors 0

                    sinon car(L) + somme_rangs_pairs(cdr(L))

3. Aspects techniques

89La machine de Peano est constituée de 2 programmes :

901. le compilateur, qui fabrique un interpréteur agrégeant l’interpréteur de base et les fonctions de l’utilisateur ;

912. l’interpréteur de base, qui évalue interactivement les expressions fournies par l’utilisateur.

92Les deux programmes sont écrits en C, principalement pour bénéficier de l’API POSIX.

3.1. Le compilateur

93Le rôle du compilateur est d’enrichir un interpréteur de base avec les fonctions de l’utilisateur. Ceci se déroule en 2 étapes :

94Voilà un exemple de la phase de compilation, avec un programme composé des 2 fonctions de la section précédentes :

  > compil exemple.peano

  Compilateur de Peano

  (C) P. Ezequel 2015

   Fichier d’entree : exemple.peano

   ................................

   Fonction somme_rangs_pairs : definition OK

   Fonction somme_rangs_impairs : definition OK

   ................................

   Fabrication de l’interpreteur : ok.

95La grammaire du langage est LL(1), ce qui permet d’utiliser un analyseur syntaxique récursif descendant. Un tel analyseur permet de détecter au plus tôt les erreurs de syntaxe. Par conséquent, il peut aussi délivrer des messages d’erreur explicites, facilement compris par des novices en programmation. Cet analyseur est utilisé par ailleurs dans un cours sur les langages formels et l’analyse syntaxique, en troisième année de Licence d’informatique.

3.2. L’interpréteur

96Une fois l’interpréteur construit par le compilateur, il peut être lancé dans un terminal. Après un message de bienvenue et un rappel des principales commandes, l’interpréteur affiche un prompt et se met en attente d’une entrée de l’utilisateur.

97L’interpréteur est une boucle classique Read - Eval - Print. Il fournit à l’utilisateur quelques commandes d’édition de ligne, avec des raccourcis à la Emacs (C-e, C-a, C-k, C-d,...) et un historique de commandes « électrique » (l’appui sur la touche "!" affiche instantanément l’historique de commandes, même en cours d’édition d’une expression).

98L’interpréteur possède trois modes, Trace, Calc et Mem, particulièrement intéressants dans le cadre d’un enseignement de la programmation fonctionnelle. Un mode est activé en tapant son nom (par exemple taper « trace » active le mode Trace), et désactivé en tapant son nom précédé de no (par exemple taper « notrace » désactive le mode Trace). Si un mode est désactivé alors qu’il n’est en fait pas activé, l’ordre de désactivation est ignoré silencieusement par l’interpréteur. Les trois modes ont la sémantique opérationnelle suivante :

991. le mode Trace (ce nom fait référence au mode du même nom en GNU-Prolog, même si bien sûr la trace d’un programme logique est bien différente de celle d’un programme fonctionnel) permet à l’utilisateur de suivre pas à pas ce qui est évalué pendant l’évaluation d’une expression. Par exemple la figure suivante montre l’évaluation de l’expression somme_rangs_pairs([1,2,3,4,5,6]) en mode Trace :

 Peano >somme_rangs_pairs([1,2,3,4,5,6])

 somme_rangs_pairs([1, 2, 3, 4, 5, 6])

    |  somme_rangs_impairs([2, 3, 4, 5, 6])

    |  |  somme_rangs_pairs([3, 4, 5, 6])

    |  |  |  somme_rangs_impairs([4, 5, 6])

    |  |  |  |  somme_rangs_pairs([5, 6])

    |  |  |  |  |  somme_rangs_impairs([6])

    |  |  |  |  |  |  somme_rangs_pairs(VIDE)

    |  |  |  |  |  |  0<==

    |  |  |  |  |  6<==

    |  |  |  |  6<==

    |  |  |  10<==

    |  |  10<==

    |  12<==

 12<==

 resultat : 12  (0 sec 33 microsec)

100Ce mode est extrêmement utile, en particulier lorsque les étudiants découvrent la récursivité. Il montre ce qui se passe quand la récursivité est utilisée, en montrant comment elle est opérationnellement gérée.

1012. Comme on peut le voir sur l’exemple ci-dessus, la machine de Peano donne le temps pris pour évaluer une expression. Cependant ce temps n’est qu’indicatif (en particulier parce qu’il s’agit du temps total d’exécution, pas du temps CPU), et aucune conclusion ne peut en être tirée. C’est pourquoi le mode Calc a été créé : quand il est activé, il affiche le nombre d’opérations primitives de la machine de Peano qu’il a fallu exécuter pour évaluer une expression (les opérations primitives sont les opérateurs arithmétiques, les comparaisons et les fonctions prédéfinies sur les listes et les arbres). Par exemple, la figure suivante montre combien d’opérations primitives sont effectuées par chacun des algorithmes de renversement de liste de la section précédente (rev1 correspond à la définition formelle, rev2 est la version utilisant myst et enfin rev3 est la fonction toto) pour renverser la liste [1,2,3,4,5,6,7,8,9,10,11,12,13,14] :

 Peano >calc

 Calcul du nombre d’operations active

 (pas de resultat)                                                                                      

                                        

Peano >rev1([1,2,3,4,5,6,7,8,9,10,11,12,13,14])

 resultat : [14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1]  

 (0 sec 5 microsec)

 435 operation(s) effectuee(s)                                                                     

                                                

Peano >rev2([1,2,3,4,5,6,7,8,9,10,11,12,13,14])

 resultat : [14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1]

 (0 sec 3 microsec)

 57 operation(s) effectuee(s)                                                                       

  

Peano >rev3([1,2,3,4,5,6,7,8,9,10,11,12,13,14])

 resultat : [14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1]

 (0 sec 266279 microsec)

 38970260 operation(s) effectuee(s)

1023. Le mode Mem affiche combien de cellules mémoire ont été utilisées pour évaluer une expression. Une cellule est l’espace nécessaire pour ranger un sommet d’un arbre binaire, ce qui montre d’abord que les listes sont, en fait, des arbres binaires, donc pas seulement des listes plates d’entiers, et ensuite que la machine de Peano ne reconnaît pas les paires pointées à la Lisp… La figure suivante montre l’utilisation simultanée des modes Calc et Mem :

 Peano >mem

 Stats memoire activees

 (pas de resultat)                                                                                      

                                                                                                                 

Peano >calc                                    

 Calcul du nombre d’operations active

 (pas de resultat)                                                                                      

                                                                                                                

Peano >rev1([1,2,3,4,5,6,7,8,9,10,11,12,13,14])

 resultat : [14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1]  

 (0 sec 5 microsec)

 119 cellule(s) utilisee(s)

 435 operation(s) effectuee(s)                                                                           

                                                                                                                

Peano >rev2([1,2,3,4,5,6,7,8,9,10,11,12,13,14])

 resultat : [14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1]  

 (0 sec 4 microsec)

 28 cellule(s) utilisee(s)

 57 operation(s) effectuee(s)                                                                      

                                                                                                               

Peano >rev3([1,2,3,4,5,6,7,8,9,10,11,12,13,14])

 resultat : [14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1]   

 (0 sec 194790 microsec)

 4427056 cellule(s) utilisee(s)

 38970260 operation(s) effectuee(s)

103Comme on peut le voir sur ces deux dernières figures, le temps d’évaluation peut varier d’une invocation à l’autre, mais le nombre d’opérations exécutées et le nombre de cellules mémoires utilisées ne change pas (ce qui est heureux, et montre que la machine de Peano est déterministe).

104L’interpréteur gère aussi les boucles infinies. Par exemple, supposons définie la fonction boucle suivante :

      boucle(N) = si N = 0 alors 1 sinon boucle(++N)

105Tout appel de la fonction boucle avec un argument non nul va engendrer une suite infinie d’appels récursifs, qui est la manifestation d’une boucle en programmation fonctionnelle. La machine de Peano va détecter ce genre de boucle, comme on peut le voir sur l’exemple ci-dessous :

 Peano >boucle(4)

 Depassement de la profondeur de recursion maximale

106Cela ne signifie pas que la machine de Peano détecte les évaluations infinies (sinon, on aurait résolu le problème de l’arrêt, qui est indécidable). En fait, l’interpréteur capture le signal SIGSEGV émis par le noyau lors d’un débordement de pile. Comme l’interpréteur est supposé sans erreurs mémoire, c’est la seule façon pour lui de recevoir ce signal. Il suffit alors de nettoyer la mémoire, et de se remettre en attente d’une nouvelle expression.

Conclusion

107La machine de Peano décrite dans les sections précédentes a été utilisée depuis environ cinq ans dans des cours de programmation fonctionnelle pour débutants. Le but était de familiariser les étudiants avec la notion de récursivité, en évitant les complications techniques (d’un point de vue pédagogique) présentes dans les langages réels, avant de leur apprendre à programmer en Lisp.

108Les retours des étudiants sont positifs. Un sondage informel des promotions 2015 et 2016 du master RIM a donné les résultats suivants (réponses synthétisées) :

109- « la syntaxe et la sémantique sont simples et clairs »

110- « bien plus facile à programmer que Lisp »

111- « une bonne introduction à Lisp, OpenMusic et Faust »

112- « les outils disponibles avec l’interpréteur sont très utiles »

113La machine de Peano est aussi utilisée, depuis beaucoup plus longtemps, en première année de Licence d’informatique, avant d’apprendre aux étudiants à programmer en CAML. Pour les collègues qui interviennent dans le cours de CAML, il y a eu un avant et un après la machine de Peano : les étudiants sont bien plus à l’aise avec la récursivité et peuvent se concentrer sur les particularités du langage lui-même.

114Il est aussi envisageable d’utiliser effectivement et utilement la machine de Peano au lycée, pour y apprendre la programmation fonctionnelle. Une conséquence possible serait de rendre la notion d’induction mathématique plus concrète, dans les cours de mathématiques.

115Cependant, dans son état de développement actuel, il manque à la machine de Peano quelques fonctionnalités utiles. Par exemple, il n’est pas possible de (re)définir une fonction à chaud, depuis l’interpréteur : il faut éditer un fichier, re-compiler et lancer le nouvel interpréteur. Dans un monde où l’utilisateur peut glisser/déposer des icônes dans des interpréteurs/compilateurs (à la Faust), cela semble un peu préhistorique. D’un autre côté, l’objectif de la machine de Peano est d’introduire la récursion et les types abstraits Liste et Arbre. Elle n’est pas faite pour développer de gros systèmes de taille industrielle. Il est donc nécessaire de trouver un équilibre entre d’une part des fonctionnalités avancées voire agréables, et d’autre part la simplicité requise pour ne pas distraire les étudiants des aspects importants de la programmation fonctionnelle.

Notes   

Citation   

Auteur   

Quelques mots à propos de :  Philippe Ézéquel