La preuve de théorèmes pour les masses (soniques)
Emilio J. Gallego Arias, Pierre Jouvelot et Benoît Pin juin 2018
juin 2018DOI : https://dx.doi.org/10.56698/rfim.489
Résumés
Résumé
Après avoir motivé la nécessité d’introduire des outils interactifs pour l’enseignement en informatique musicale et, plus généralement, dans les disciplines scientifiques, nous décrivons jsCoq, notre nouvelle interface utilisateur pour le logiciel de preuve mathématique Coq. Cet outil fournit aux enseignants un moyen efficace pour concevoir et mettre en œuvre des cours qui combinent textes, audio, images et preuve interactive de théorèmes. Nous présentons deux études de cas d’utilisation dans le domaine audio et les résultats d’une évaluation de jsCoq sur le terrain.
Notes de la rédaction
Cet article est la traduction française de « Bringing Theorem Proving to the (Sonic) Masses », publié dans Innovative Tools and Methods for Teaching Music and Signal Processing, L. Pottier (Ed.), Presses des Mines, 2017.
Les auteurs souhaitent remercier les nombreux participants aux deux cours Coq mentionnés dans l’article pour leurs précieux commentaires. Une partie du développement de jsCoq a été financée par le projet ANR FEEVER.
Texte intégral
Introduction
1Si mathématiques et musique étaient déjà des domaines académiques liés dans la Grèce antique, l’époque contemporaine et numérique a définitivement renforcé ce lien centenaire. L’informatique peut, au niveau fondamental, être considérée comme une branche des mathématiques, à savoir ce qu’on appelle les « mathématiques constructives » (Martin-Löf, 1985). Étant donné que la plupart des créations musicales contemporaines profitent, d’une manière ou d’une autre, des techniques et des outils de traitement du signal numérique (Digital Signal Processing, ou DSP) fondés sur l’ordinateur, elles sont à la fois des œuvres d’art et des entités mathématiques.
2Si, dans le passé, les musiciens s’assuraient à l’oreille de la « justesse » des opérations traditionnelles, c’est-à-dire analogiques, de la musique et du traitement du son (c’est toujours le cas pour les instruments acoustiques), les compositeurs et ingénieurs audio peuvent aujourd’hui profiter du pouvoir du raisonnement mathématique pour confirmer que les artefacts audio produits numériquement « sonneront comme ils doivent le faire », que ce soit lors de l’exécution de transformations sonores spectrales complexes ou de filtrages simples via des programmes informatiques.
3Étant donné que certaines propriétés sonores clés comme, par exemple, l’absence de distorsion ou la conservation de l’énergie correspondent à de telles propriétés mathématiques, on peut envisager d’utiliser des méthodologies informatiques de démonstration largement développées telles que la vérification de modèles ou les vérificateurs de théorèmes, pour s’assurer que ces propriétés sont vérifiées par les algorithmes de traitement de la musique développés par les utilisateurs.
4Se familiariser avec les spécificités de ces environnements et de leurs outils associés est une tâche difficile ; l’un des objectifs qui stimulent le développement de jsCoq (Gallego Arias et al., 2016), une interface en ligne pour l’assistant Coq1 (Bertot & Castéran, 2004], est de faciliter l’apprentissage des connaissances requises pour maîtriser de telles techniques.
5Dans cet article, nous motivons tout d’abord la nécessité d’introduire des approches et outils pédagogiques nouveaux pour aborder cette vision mathématique de la musique informatique et de l’ingénierie audio. Plus largement, nous décrivons une approche de l’éducation en STEM (Science, technologie, ingénierie et mathématiques) où l’interaction serait au cœur du processus d’apprentissage. Nous présentons ensuite l’assistant de preuve Coq et la nouvelle interface utilisateur jsCoq que nous avons conçue et mise en œuvre. Pour fournir des informations pratiques sur l’utilité de jsCoq en tant qu’instrument pédagogique axé sur la musique et le son, nous décrivons deux études de cas dédiées aux opérations typiques de traitement audio : (1) la dérivation de certaines propriétés de la transformée de Fourier discrète, un cheval de bataille du traitement audio spectral ; et (2) la preuve qu’un filtre audio simple mis en œuvre dans Faust2 (Orlarey et al., 2004) est stable. Nous avons également évalué jsCoq sur le terrain, en l’utilisant pour des tutoriels et des classes ; nous présentons brièvement les observations effectuées. Enfin, nous concluons et soulignons les travaux futurs possibles.
1. Motivations
6Le point de départ du projet jsCoq est notre désir de relier la démonstration de théorèmes interactive, le traitement du signal et l’informatique musicale (textuelle). Selon ce point de vue, ces champs peuvent être compris comme ayant un certain nombre de points en commun ; par exemple, la preuve de théorèmes interactive et les systèmes informatiques de codage en temps réel (live coding) tels que SuperCollider3(McCartney, 2002) reposent sur un schéma d’interaction fondé sur une interface de boucle Lecture/Évaluation/Impression (boucle Read/Eval/Print, ou REPL).
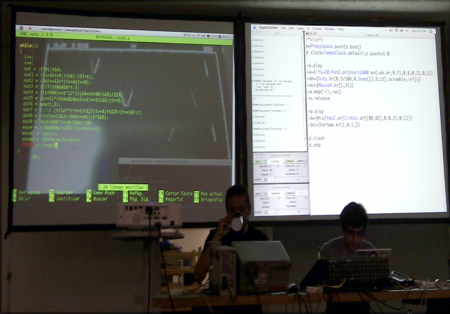
7Dans un tel cadre, l’utilisateur et l’ordinateur sont étroitement liés dans un protocole de type commande-réponse : l’utilisateur entre une commande ou une expression ; celle-ci est évaluée ou effectuée par l’ordinateur ; en fonction de la sortie résultante (ici typiquement audio), l’utilisateur réitère le processus, qui peut même se produire en public pendant les sessions de codage en direct (voir la figure 1). Dans le domaine du traitement du signal, la construction progressive des programmes peut ne pas atteindre le même niveau d’interaction ; cependant, il est certain que la conception de nombreux systèmes industriels utilise bon nombre d’expérimentations successives, MATLAB4 étant l’outil privilégié en ce domaine.
1.1. Accessibilité et interactivité
8Les textes d’introduction et de formation sont souvent élaborés en utilisant le style de programmation dit « littéraire » (Knuth, 1984) : le programme et le texte sont mélangés dans une structure cohérente que le lecteur/programmeur/musicien peut découvrir. Certains environnements tels que SuperCollider ou MATLAB fournissent en effet une interface spéciale prenant en charge le code littéraire ; d’autres, comme de nombreux vérificateurs de théorèmes, fournissent des résultats différenciés. L’utilisateur doit ensuite choisir entre les présentations textuelle ou exécutable.
Figure 1. SuperCollider live coding
Source : http://pawfal.org
9Bien qu’une présentation correcte et la cohérence des divers documents constituent une condition indispensable pour la production de matériel pédagogique, l’accessibilité est essentielle à son utilité pratique. De fait, des efforts importants sont consacrés ces temps-ci, dans tous les domaines, à la publication de systèmes informatiques plus conviviaux et accessibles, des interfaces utilisateur fondées sur le Web aux versions mobiles. Dans le même ordre d’idées, nous croyons fermement que l’accessibilité pour les utilisateurs devrait jouer un rôle crucial dans la conception de nouveaux outils : un nouvel environnement, même attrayant, attirera peu l’attention s’il est difficile à utiliser. Dans l’enseignement, on passe pas mal de temps à aider les utilisateurs à résoudre des problèmes sans intérêt liés aux plateformes, et il n’est pas rare d’assister à de courtes sessions de tutoriels où certains assistants ne peuvent même pas parvenir à faire fonctionner les outils.
10En revenant à notre dessein original, un scénario naturel se dessine : imaginez un programmeur/étudiant en DSP qui souhaite explorer une théorie du filtrage formalisée avec un démonstrateur interactif de théorèmes. En principe, cela ne devrait pas poser de problèmes, et nous croyons qu’un tel étudiant pourrait tirer grandement parti des connaissances fondamentales sur les techniques mathématiques et déductives utilisées ; en outre, l’utilisation de la démonstration de théorèmes interactive se rapproche assez du « jeu vidéo », un excellent atout de motivation.
11Cependant, de tels utilisateurs seront rapidement confrontés à un problème : pour s’entraîner pendant quelques heures et commencer à obtenir quelques intuitions sur le processus de preuve mécanisé, ils devront passer quelques après-midi pénibles à se battre avec outils et bibliothèques pour les installer. En effet, plus la configuration est évoluée, plus l’utilisateur aura de bibliothèques et de modes spéciaux à installer. Dans un monde idéal, cela devrait fonctionner de manière transparente ; cependant, en réalité, on en est loin.
1.2. Programmation et mathématiques
12Notre deuxième motivation pour concevoir jsCoq vient de la volonté de renforcer le lien entre la programmation, la démonstration de théorèmes et les mathématiques, en particulier dans le domaine du traitement du signal audio. En effet, les démonstrateurs de théorèmes constructifs tels que Coq fournissent un tel lien. Imaginez que l’on souhaite prouver une proposition P, la manière standard est d’utiliser une relation d’implication telle que « Q implique P », puis de vérifier que P est en effet impliqué par elle en prouvant récursivement Q (qu’on espère plus simple.) Ces relations sont généralement définies par un ensemble de règles. Cependant, les démonstrateurs de théorèmes constructifs vont un peu plus loin, ce qui nous oblige à fournir des preuves pour P. On écrit cela « p : P », où p est un programme de type P. Le lecteur familier avec la programmation fonctionnelle typée reconnaîtra immédiatement ce schéma, qui est fondé sur le fait de considérer le programme p comme preuve pour P.
13Fait intéressant, on pourrait dire que le DSP, en particulier dans l’audio, est, en quelque sorte, l’art d’approcher les processus mathématiques et physiques avec des programmes qui correspondent parfaitement à ce paradigme de preuve et de programme. À notre avis, cela fait des démonstrateurs de théorèmes constructifs tels que Coq des outils parfaits pour explorer le DSP. Le lien entre Coq, en particulier son extension Ssreflect, et l’informatique musicale mérite clairement d’être étudié (Gallego et al., 2015).
14Pourtant, aussi séduisant que soit ce concept, la réalité de la démonstration de théorèmes constructive n’est certainement pas aussi brillante. Les notations mathématiques et les diagrammes sont difficiles à adapter aux programmes, et ce n’est que récemment (Gonthier et al., 2013) que certaines notions mathématiques de base telles que la théorie de la représentation ont été formalisées de manière raisonnable et lisible.
15Comme dans le cas précédent d’accessibilité, les médias et les outils sont à l’origine de nombreuses limitations. Les assistants de preuve héritent profondément de leurs racines fondées sur des contenus textuels adaptés aux terminaux, ayant des difficultés à mettre en œuvre les stratégies de représentation plus riches dont nous croyons que les pratiques d’enseignement modernes bénéficieront.
1.3. Hypothèse
16Comment pouvons-nous essayer de répondre à tant de préoccupations ? Nous croyons que le Web moderne offre une opportunité exceptionnelle pour commencer à aborder ces problèmes. Nous souhaitons fournir aux utilisateurs une solution d’apprentissage transparente et accessible partout qui permettrait, non seulement à des environnements complexes tels que Coq d’être immédiatement opérationnels, mais aussi une expérience d’apprentissage multimédia plus riche pour les utilisateurs. L’avènement de plates-formes Web avancées normalisées (HTML5)5 et de puissants mécanismes multimédias d’interaction avec les utilisateurs (texte, graphiques, audio, calculs effectués sur le client) font d’un tel objectif une réalité plausible.
17De fait, même si jsCoq est un outil de travail ayant un objectif tout à fait spécifique, nous croyons qu’il devrait être considéré comme une preuve de concept de ce qui est, en réalité, notre contribution principale ici : une vision de la façon dont les choses devraient être faites dans le monde enseignant de demain.
2. Apprentissage interactif en STEM
18La pensée computationnelle a gagné du terrain dans le domaine de l’éducation en STEM6 (Science, technologie, ingénierie et mathématiques), où les systèmes interactifs se sont révélés être des éléments prometteurs (Weintrop et al., 2014). Nous mettons brièvement en perspective ici l’approche interactive fondée sur des systèmes que nous préconisons pour l’amélioration de l’enseignement dans nos domaines d’intérêt, à savoir les mathématiques, l’informatique et l’audio. Nous croyons que de tels systèmes peuvent avoir un impact significatif sur la participation et la motivation des étudiants, en offrant une expérience utilisateur plus vivante lorsqu’ils abordent des concepts difficiles et abstraits.
2.1. Mathématiques
19L’enseignement des mathématiques est considéré comme une tâche difficile, du point de vue du curriculum et de la pédagogie (Lockhart, 2009). En particulier, on s’accorde sur la nécessité de nombreuses heures de pratique et d’exercice par des élèves concentrés afin d’obtenir de bons résultats7.
20L’accès généralisé aux médias sur demande nous a apporté une myriade de cours en ligne, qui semblent très populaires dans la communauté étudiante (voir, par exemple, l’Académie Khan8), et des tests sur le Web que les élèves peuvent utiliser pour se corriger eux-mêmes, également couramment utilisés par les cours massifs en ligne (Massive Open Online Courses,ou MOOCs).
21Cependant, ce n’est que récemment que le développement de systèmes d’enseignement mathématique vraiment interactifs, comme Edukera9 et Mathbox10, a réussi à décoller. Si une évaluation précise de l’impact réel (le cas échéant) de ces systèmes récents sur la motivation des étudiants et la courbe d’apprentissage à long terme est toujours en cours, cette recherche sera clairement utile pour nous aider à développer la conception de jsCoq.
2.2. Informatique
22En généralisant largement, l’enseignement de l’informatique peut être considéré comme très similaire à l’enseignement des mathématiques, en particulier dans les matières théoriques. Cependant, du côté pratique des choses, un nouveau composant expérimental apparaît : les élèves doivent écrire et exécuter des programmes. Ceux-ci vont souvent se tromper, et donc une boucle d’essai et erreur se crée dans laquelle l’élève progresse graduellement, à la fois par l’expérience et par l’acquisition de nouveaux modèles et techniques de programmation.
23Un texte très influent est The Art of Computer Programming (Knuth, 1968) ; il mélange code, mathématiques et texte dans un seul format, mettant en avant la notion de « programmation littéraire », un style dans lequel le code est seulement une partie d’un document plus large et cohérent. Malgré son attrait, l’approche littéraire n’est pas aussi présente que nous croyons qu’elle devrait l’être, principalement en raison du manque d’environnements vraiment interactifs.
24Des progrès importants ont été réalisés par le passé ; des systèmes tels que PILeT (Alshaigy, 2013) aident les élèves à apprendre des langages de programmation, ici python, tandis que des techniques de visualisation d’algorithmes telles que celles présentées dans OpenDSA (Fouh et al., 2014) peuvent être utilisées pour animer des algorithmes et des opérations de manipulation de structures de données. Pourtant, il est facile pour les outils éducatifs interactifs fondés sur l’informatique d’être dépassés dans le monde si dynamique des systèmes d’exploitation et des environnements graphiques (Graphical User Interface, ou GUI). Toutefois, des avancées technologiques récentes améliorant les performances ont été obtenues sur les principales plates-formes de navigation, par exemple HTML5 et les programmes côté client. Ils ont ouvert la voie à la naissance d’environnements pédagogiques sur le Web plus accessibles (et, espérons, plus stables). Même si la plupart de ces environnements en ligne, par exemple Codecademy11 ou même jsCoq, ne sont pas encore assez puissants pour prendre totalement en compte l’enseignement de premier cycle, ils approchent rapidement d’un état utilisable.
2.3. DSP audio
25À l’intersection des mathématiques, de l’informatique et de la physique, le DSP audio hérite de la pratique de tous ces domaines. Cependant, un troisième axe, expérimental, apparaît : l’étudiant doit écouter les résultats. En effet, le réglage par l’oreille des algorithmes de traitement audio est fréquent, et être capable de relier l’effet d’une modification d’un programme à la modification correspondante du son résultant semble essentiel.
26Dans ce domaine particulier, nous irions même jusqu’à dire que l’utilisation de la programmation littéraire est beaucoup plus fréquente, de nombreux environnements audio-dédiés étant directement fondés sur elle. Contrairement à d’autres domaines de l’informatique, il est essentiel d’exécuter les programmes ; ainsi, les environnements populaires tels que SuperCollider ou le système Audio Toolbox12 de MATLAB supportent de manière native un format de document mixte : à mesure que l’élève lit le chapitre du document, il pourra profiter d’un système en cours d’exécution, en direct, sonore. Notre technologie jsCoq a pour intention de fournir une expérience utilisateur similaire dans un environnement Web.
2.4. Preuve interactive de théorèmes
27Nous concluons avec quelques brefs commentaires sur les méthodes d’enseignement utilisées dans la preuve de théorèmes interactive (Interactive Theorem Proving, ou ITP). Étant donné que ce domaine particulier est beaucoup plus jeune que les précédents, la méthodologie d’enseignement spécifique est moins développée.
28Comme nous l’avons mentionné ci-dessus, dans la preuve de théorèmes, l’utilisateur travaille dans une boucle d’action-réaction étroitement couplée avec l’ordinateur. En règle générale, l’utilisateur fournira à l’ordinateur certaines étapes ou heuristiques, et l’ordinateur vérifiera leur validité, guidant peut-être les étapes futures. Ainsi, nous sommes confrontés ici à une situation similaire à celle rencontrée dans le DSP, où un livre purement textuel fournira peu d’indices pour l’apprentissage ; l’interaction avec le système est essentielle à une bonne compréhension. En outre, un assistant de preuves peut fournir des informations de guidage précieuses aux étudiants, car ces derniers peuvent vérifier l’exactitude de leurs propres solutions ; bien sûr, le professeur peut encore, et devrait, commenter la méthode particulière choisie.
29Une autre difficulté majeure se rencontre lorsque l’élève n’est pas habitué à la notion même de preuve. L’expérience suggère qu’il vaut mieux considérer comme distincts l’enseignement de la façon de faire des preuves et celui d’utiliser les outils pour faire des preuves : la première requiert une réflexion et une organisation de haut niveau, alors que la seconde nécessite une attention aux détails et à la connaissance du système formel particulier utilisé.
30Mais même les utilisateurs expérimentés dans l’art de faire des preuves auront des difficultés à suivre les étapes de la preuve si les commentaires de l’outil ne sont pas présents. Par exemple, nous avons récemment observé un lecteur occasionnel de la version papier d’un texte sur la bibliothèque Coq/Ssreflect Mathematical Components13. Elle a vite été perdue quand les « opérations de sélection de termes », qui précisent une partie de l’objectif à remplacer ou à généraliser, ont été abordées. Ce type d’opérations – trivial à comprendre si l’accès interactif à l’outil est fourni – est la raison pour laquelle la plupart des publications sur la démonstration de théorèmes sont écrites dans un style de programmation littéraire.
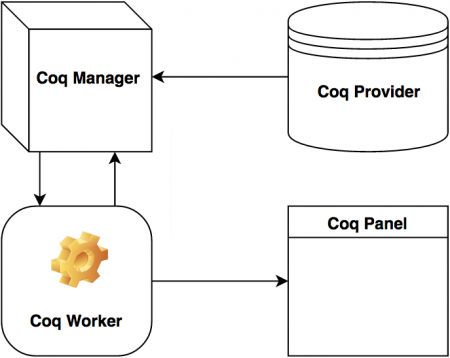
Figure 2. Composants jsCoq
3. De Coq à jsCoq
31Nous nous concentrons désormais, pour le reste de cet article, sur notre outil, à savoir l’assistant de preuve Coq. Avec plus de trente ans d’histoire, Coq est un outil largement utilisé en informatique et l’un des premiers de son genre à être enseigné en dehors de l’environnement hautement spécialisé d’une classe.
32Le texte qui a démocratisé l’enseignement de Coq, au moins pour les informaticiens, est Software Foundations (Pierce et al., 2016), un livre complet développant un canon de base sur les langages de programmation en utilisant Coq. Ce livre est entièrement écrit dans le style littéraire et utilise l’outil de documentation Coq « coqdoc » pour générer une version HTML. Cependant, on pourrait dire que la version HTML est presque anecdotique, car le livre doit être entièrement lu en même temps que le code est exécuté. Le livre est donc limité au texte, et, même si des efforts considérables sont faits pour utiliser le système de notation extensible de Coq, de nombreux diagrammes et explications paraissent bien rudimentaires, comparés à leurs homologues habituellement mis en page en utilisant le système LaTeX.
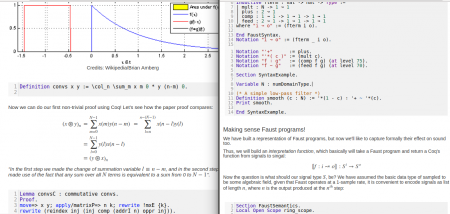
Figure 3. Exemples jsCoq pour la DFT (à gauche) et Faust (à droite)
33Comme indiqué précédemment, nous nous proposons, avec jsCoq, d’adopter l’approche inverse. Nous allons commencer par un document – dans notre cas, en HTML – et nous allons l’étendre avec la possibilité d’interagir avec Coq. Ainsi, le flux de lecture sera énormément amélioré, et l’étudiant pourra toujours interagir avec Coq au besoin.
3.1. Survol technologique de jsCoq
34Le langage de programmation choisi pour jsCoq est JavaScript, un outil natif de toutes les plateformes Web modernes. La tâche principale de jsCoq sera de lier les documents littéraires au niveau de l’utilisateur à la notion de document Coq. Les documents Coq, appelés scripts de preuve, sont des séquences de définitions textuelles et d’appels à des tactiques, qui définissent des objets et guident Coq dans l’élaboration d’une preuve.
35Nous appelons une pièce de texte logique individuelle comprise par Coq une portée (span). Les portées sont soumises à Coq par jsCoq pour créer le script de preuve, et Coq, en retour, fournit des commentaires sur le résultat de chaque commande présente dans le document construit de son côté. En particulier, les commandes peuvent réussir, échouer ou générer différents types de sortie que l’utilisateur doit voir.
36Les portées Coq sont extraites du document côté client par un fournisseur (provider)Coq (Figure 2), qui fait partie de jsCoq. L’interface du fournisseur est générique, permettant d’utiliser le système avec différents éditeurs ou environnement (frameworks) Web ; tout ce qu’ils doivent mettre en œuvre est une façon d’extraire et de marquer les parties correspondantes d’un script. La version actuelle de jsCoq est livrée avec un fournisseur standard, un éditeur de texte fondé sur le logiciel libre CodeMirror14, mais d’autres options apparaîtront à l’avenir.
37Au cœur de jsCoq se trouve le gestionnaire Coq (Manager). Le gestionnaire est chargé de coordonner les portées provenant du document et les réponses de Coq. Il s’occupe de l’invalidation et de la soumission des portées, ainsi que de la gestion du processus Coq. Ce processus Coq, appelé ouvrier Coq (Worker), est un emballage personnalisé du système Coq standard lui-même, compilé en JavaScript en utilisant la technologie15 de transpilation16 js_of_ocaml ; nous exécutons donc un Coq non modifié dans le navigateur. Nous proposons également un petit panneau Coq (Panel) détachable pour l’affichage des objectifs, la recherche des théorèmes existants, etc. L’utilisation de ce panneau est facultative et nous pensons que les documents les mieux intégrés ne l’utiliseront pas.
38Nous souhaitons terminer cette section sur une note légèrement technique, mais à notre avis très importante. Nous avons consacré beaucoup d’efforts à rendre la notion de document Coq plus conviviale que celle utilisée sur le Web. Au début du projet jsCoq, le modèle de document Coq et le protocole d’interaction n’étaient pas très bien adaptés au modèle de document DOM utilisé par les navigateurs, même si des progrès avaient été accomplis ces dernières années vers un modèle plus réactif. Après beaucoup d’essais et d’erreurs, et des commentaires précieux provenant des utilisateurs, nous avons réussi à développer le modèle Coq pour qu’il devienne beaucoup mieux adapté à DOM. À l’heure actuelle, le gestionnaire Coq n’est rien d’autre qu’une mince enveloppe recouvrant le modèle de document Coq que nous avons défini, ce qui simplifie considérablement le système.
3.2. Utiliser jsCoq
39Tout ce qu’un enseignant de STEM qui veut écrire des documents pédagogiques sur le Web qui interagissent avec Coq a à faire est d’inclure quelques lignes JavaScript, d’éventuellement définir quelques options et enfin d’indiquer les parties du document qui doivent être visibles pour Coq. Ensuite, le panneau Coq sera joint au document et l’utilisateur pourra commencer l’interaction. Pour faciliter le développement de contenus pédagogiques, les documents jsCoq peuvent être générés automatiquement à partir d’un fichier Coq en utilisant une version modifiée de l’outil de documentation « coqdoc » standard. Nous avons utilisé cet outil17 pour générer les versions jsCoq de textes existants adaptés à coqdoc.
40Une caractéristique cruciale de l’approche jsCoq est sa nature autonome. Chaque document jsCoq comprend une version privée de Coq et une copie de toutes les bibliothèques utilisées. Cela signifie que nous n’avons pas à nous soucier des incompatibilités ou conflits avec les versions futures. Cette approche autonome est particulièrement utile pour l’enseignant désireux d’utiliser des composants externes. Auparavant, l’installation de Coq et de ses systèmes associés pouvait prendre beaucoup de temps pour l’élève. Maintenant, ils apparaissent tous en un seul instant. Notre outil jsCoq prend en charge plus de quinze paquets et modules complémentaires Coq par défaut et est devenu une plate-forme pratique pour illustrer rapidement de nouveaux développements. Nous présentons ci-dessous quelques exemples inclus dans notre outil, par défaut.
4. Deux études de cas pour jsCoq
41Nous décrivons dans cette section deux développements récents liés à l’audio qui ont bénéficié de jsCoq. Nous fournissons des captures d’écran de jsCoq à une étape particulière de son utilisation et donnons quelques explications de ce qui est affiché. Cependant, la vraie nature des exemples ne peut naturellement être appréciée qu’en interagissant avec l’outil. Ces exemples sont facilement accessibles à partir de la page principale du projet jsCoq. Notez que, outre nos exemples, la page du projet jsCoq comprend une version expérimentale de Software Foundations, en plus de quelques extraits d’un autre livre.
4.1. Transformée de Fourier discrète
42Le premier exemple est une formalisation constructive d’un classique en DSP audio, à savoir la transformée de Fourier discrète (Discrete Fourier Transform, ou DFT) ; nous suivons ici la présentation fournie dans Mathematics of the Discrete Fourier Transform (Smith, 2007). La figure 3 (gauche) constitue une capture d’écran d’une fenêtre de navigateur qui affiche une page HTML enrichie par jsCoq et traitant de la notion de convolution. Ici, la définition dans Coq de l’opération de convolution convs18 et la preuve du lemma convsC, qui stipule qu’une telle opération est commutative, sont directement gérées par jsCoq (dans les boîtes grises) ; cette zone de texte peut être directement éditée et exécutée de manière interactive par l’utilisateur. Notez la manière dont cette preuve Coq est précédée de l’explication mathématique correspondante (mise en forme à l’aide de MathJax.js19) ; l’élève peut donc les mettre facilement en correspondance. Des images peuvent également être incluses dans des documents hybrides fondés sur HTML pour mieux illustrer un concept, comme ici où les graphiques de deux fonctions f et g sont affichés pour expliquer un point particulier concernant les informations de convolution.
4.2. Filtrage audio en Faust
43Dans le second exemple (voir les extraits de la figure 3, droite), nous développons la formalisation en Coq d’une preuve de stabilité pour un filtre simple exprimé dans le langage de traitement audio Faust (Gallego Arias et al., 2015). Dans la première zone de texte Coq, on peut apercevoir comment une version simplifiée de la syntaxe Faust est définie via une construction inductive Coq, où l’arité des processeurs de signaux Faust est utilisée pour typer chaque constructeur de données (par exemple, l’expression + Faust sera encodée comme une expression Coq plus dont le type fterm 2 1 indique qu’il faut deux signaux d’entrée pour produire une sortie). Ensuite, la construction Notation est utilisée pour définir du sucre syntaxique pour les termes typés Coq représentant la syntaxe Faust ; notez comment cette fonction Coq, pratique, peut faciliter l’entrée par l’utilisateur d’expressions de test dans un prototype aussi simple. Enfin, l’opération de filtrage smooth est définie ; il s’agit d’une boucle de rétroaction simple, où le paramètre c est utilisé comme facteur d’amortissement. Ici, l’existence dans Coq de notations extensibles nous permet de représenter chaque terme de manière étroitement lié à sa syntaxe originale Faust.
44La deuxième partie du document affiché dans la figure 3, à droite, est le début de la gestion sémantique de la syntaxe Faust définie ci-dessus. Il est précédé d’un bref texte qui introduit le problème, combiné à une formule mathématique définissant la notion de sémantique pour les processeurs de signaux Faust, considérés ici comme des fonctions d’un tuple de signaux d’entrée (la taille dynamique de tuple i doit correspondre à l’arité présente dans les informations de typage) vers un tuple de signaux de sortie. Encore une fois, comme dans notre première étude de cas sur la DFT, les commentaires, les éléments mathématiques et les preuves constituent une présentation agréable sous forme de tutoriel, ici de certaines bases de la vérification de logiciel appliquée au traitement audio.
5. Evaluation sur le terrain
45En ce qui concerne l’utilisation réelle dans des salles de classe, jsCoq a été utilisé dans deux cours réels depuis la publication d’un premier prototype opérationnel.
-
Le premier cours, lors de l’école d’hiver Coq « Advanced Software Verification and Computer Proof », a eu lieu à Sophia-Antipolis, en France, en 2016, avec une trentaine d’étudiants pendant une semaine. Les commentaires ont été très positifs. En effet, notre outil a été une source d’amélioration par rapport aux éditions précédentes de l’école, car les étudiants pouvaient se concentrer sur les preuves dès le premier jour, ce qui contrastait avec les autres éditions, dans lesquelles une journée complète était souvent dédiée à la mise en place du système Coq sur les machines des étudiants.
-
Le deuxième cours était un tutoriel d’une demi-journée consacré à la bibliothèque Mathematical Components, donné lors de la conférence ITP2016 à Nancy, en France. Encore une fois, l’expérience a été très positive, l’outil fonctionnant correctement et tous les intervenants pouvant interagir avec Coq en utilisant jsCoq.
46En ce qui concerne les aspects négatifs, alors que la plupart des participants considéraient que l’outil était utilisable – il n’a jamais cessé de fonctionner comme prévu –, il y a eu des plaintes concernant la maturité de l’interface utilisateur. Sur ce point, nous sommes limités par la main-d’œuvre, mais, comme les fondements de l’outil semblent solides, nous espérons progressivement améliorer ce composant de jsCoq. Compte tenu de ces expériences positives, au moins deux autres cours et tutoriels sont prévus pour la fin 2016.
Conclusion
47Dans cet article, après avoir motivé la nécessité de nouvelles approches et outils pédagogiques interactifs pour l’éducation en matière d’informatique musicale, d’ingénierie audio et de STEM, nous avons présenté notre nouvelle interface utilisateur autonome pour l’assistant mathématique Coq : jsCoq. Cette technologie d’enseignement de pointe fournit un moyen efficace permettant aux enseignants intéressés par les mathématiques de concevoir et mettre en œuvre des documents hybrides autonomes qui combinent des éléments de preuve de théorèmes interactive, de texte, d’image ou d’audio. Nous pensons que cela facilitera l’introduction de l’enseignement interactif dans les matières STEM. Nous avons décrit deux études de cas consacrées aux opérations typiques de traitement audio et présenté les résultats assez positifs d’une évaluation sur le terrain de jsCoq.
48À long terme, bien sûr, il reste à voir quel impact jsCoq aura sur le champ de l’enseignement de Coq lui-même. D’une part, nous pouvons affirmer qu’il a déjà eu une certaine influence sur ce que les étudiants et les enseignants peuvent désormais attendre, et l’outil a suscité l’intérêt de nombreux partenaires. D’autre part, de nombreuses améliorations sont nécessaires pour épauler l’enseignement à grande échelle de Coq ; en particulier, l’interface utilisateur et les outils de génération de documents ont besoin de plus de finition. Nous avons cependant atteint le point où nous croyons que jsCoq restera maintenant avec nous pendant longtemps.
Bibliographie
Alshaigy B. (2013), « Development of an interactive learning tool to teach python programming language », in Proceedings of the 18th ACM Conference on Innovation and Technology in Computer Science Education (ITiCSE’13), ACM, NY, USA, p. 344-344.
Bertot Y. & P. Castéran (2004), Interactive Theorem Proving and Program Development. Coq’Art: The Calculus of Inductive Constructions, Springer.
Fouh E., Karavirta V., Breakiron D. A., Hamouda S., Hall S., Naps T.L. & C.A. Shaffer (2014), « Design and architecture of an interactive eTextbook – The OpenDSA system », Science of Computer Programming, volume 88, p. 22-40.
Gallego Arias E. J., Hermant O & P. Jouvelot (2015), « A Taste of Sound Reasoning in Faust », Thirteenth Linux Audio Conference, Mainz, Germany.
Gallego Arias E. J., Pin B. & P. Jouvelot (2016), « jsCoq: Towards Hybrid Theorem Proving Interfaces », 12th International Workshop on User Interfaces for Theorem Provers, Coimbra, Portugal.
Gonthier G., Asperti A., Avigad J., Bertot Y., Cohen C., et al. (2013), « A Machine-Checked Proof of the Odd Order Theorem », 4th Conference on Interactive Theorem Proving (Rennes, France), LNCS 7998, Springer, p. 163-179.
Knuth D. E. (1968), « The Art of Computer Programming », Boston (MA), Addison-Wesley.
Knuth D. E. (1981), « Literate Programming », The Computer Journal, 27(2), p. 97-111.
Lockhart P. D. (2009), « A Mathematician’s Lament », New York, Bellevue Literary Press.
Martin-Löf P. (1985), « Constructive mathematics and computer programming », Proc. of a discussion meeting of the Royal Society of London on Mathematical logic and programming languages, C.A.R. Hoare and J.C. Shepherdson (Eds.), Prentice-Hall, Inc., Upper Saddle River, NJ, USA, p. 167-184.
McCartney J. (2002), « Rethinking the computer music language: SuperCollider », Computer Music Journal, 26(4), p. 61-68.
Orlarey Y., Fober D. & S. Letz (2004), « Syntactical and semantical aspects of Faust », Soft Computing, 8(9), p. 623–632.
Pierce B. C., Azevedo de Amorim A., Casinghino C., Gaboardi M., Greenberg M., Hriţcu C., Sjöberg V. & B. Yorgey (2016), « Software Foundations », https://www.cis.upenn.edu/~bcpierce/sf/current/index.html (accessed on line 2016/11/3)
Smith J. O. (2007), « Mathematics of the Discrete Fourier Transform (DFT) with Audio Applications », Second Edition, W3K Publishing.
Weintrop D., Beheshti E., Horn M. S., Orton K., Trouille L., Jona K. & U. Wilensky (2014), « Interactive Assessment Tools for Computational Thinking in High School STEM Classrooms », 6th International Conference, INTETAIN 2014, Chicago, IL, USA, July 9-11, p. 22-25.
Notes
2 Nous avons utilisé ici le langage de programmation audio fonctionnel Faust, mais tout autre langage de musique informatique, avec une sémantique mathématique précisément définie, aurait pu en théorie être utilisé. Pourtant, la sémantique fonctionnelle propre de Faust aide à faciliter les preuves.
3 http://www.pawfal.org/dave/blog/tag/supercollider/
6 http://www.stemedcoalition.org
7 http://nautil.us/issue/40/learning/how-i-rewired-my-brain-to-become-fluent-in-math-rp
8 https://www.khanacademy.org/
10 https://gitgud.io/unconed/mathbox
12 http://www.mathworks.com/products/audio-system/
13 https://math-comp.github.io/math-comp/
15 https://ocsigen.org/js_of_ocaml/
16 On parle généralement de transpilation lorsqu’un langage est compilé dans un autre langage fournissant approximativement le même niveau d’abstraction.
17 https://github.com/ejgallego/udoc
18 Remarquez comment la Definition en Coq de convs pour deux signaux x et y, encodés en Coq par des matrices Nx1 d’échantillons, est proche de sa définition mathématique usuelle sous forme d’un signal, ici une suite de colonnes de 1 échantillon indexée par n, contenant les sommes sur m des produits de x(m, 0) avec y(n-m, 0).