Du scénario linéaire aux scénarios multiples pour le logiciel i-score dans le projet OSSIA
Myriam Desainte-Catherine novembre 2016
novembre 2016DOI : https://dx.doi.org/10.56698/rfim.410
Résumés
Résumé
Cet article présente l’étude qui a conduit à l’extension du modèle de scénario linéaire du logiciel i-score vers un modèle non-linéaire, c’est-à-dire comportant des conditions exprimant des alternatives dépendant de l’exécution du scénario en temps réel. Cette étude s’est déroulée dans le cadre du projet ANR OSSIA. Nous présentons d’abord le modèle temporel initial, les modèles théoriques logico-temporels proposés en début de projet, puis les échanges avec les utilisateurs, et enfin les problèmes à résoudre et le choix final.
Index
Index de mots-clés : systèmes multimédia interactifs, écriture de scénarios non linéaires, exécution de scénarios non linéaires, modèle de temps arborescent.Notes de l'auteur
Ce travail s’est déroulé dans le cadre du projet ANR OSSIA (Open Scénario System for Interactive Application, ANR-05-SSIA-0016-01) coordonné par le GMEA, avec pour partenaires le LaBRI, BLue Yeti, l’ENJMIN et RSF, et avec la participation active des artistes Pascal Baltazar, Renaud Rubiano, Julien Rabin et des ingénieurs et chercheurs Théo de la Hogue, Clément Bossut, Jaime Chao, Jean-Michaël Celerier, Nicolas Vuaille, Nicolas Hincker et Jaime Arias.
Texte intégral
1 Introduction
1Cet article présente l’étude qui a conduit à l’extension du modèle de scénario linéaire du logiciel i-score vers un modèle non-linéaire. Cette étude s’est tenue durant les premiers mois du projet ANR OSSIA [BdlHDC14, MDC13], s’étendant sur 3 ans à partir du 1er octobre 2012 et confrontant scientifiques, ingénieurs et utilisateurs. La présentation de ce travail se veut intuitive et non formelle mettre en évidence l’esprit et la logique qui ont conduit à l’élaboration du modèle retenu.
1.1 Le logiciel i-score et le projet OSSIA
2Le logiciel i-score1 est un séquenceur intermedia interactif. Il permet d’organiser sur une timeline des événements et de coordonner l’exécution de processus pilotant divers medias. Une telle organisation, composée d’événements, de processus, de paramètres et de relations temporelles est appelée un scénario. Certains événements sont dits interactifs car ils peuvent être déclenchés dynamiquement lors de l’exécution (leur déclenchement dépend de l’exécution), alors que les autres sont déclenchés automatiquement par le système (leur déclenchement ne dépend que des relations temporelles écrites dans le scénario). Le logiciel i-score est utilisé par des artistes pour réaliser des installations interactives multimedias2.
3L’utilisation d’une timeline pour éditer le scénario est une contrainte du projet OSSIA mais aussi une originalité permettant de mettre à la portée d’utilisateurs non programmeurs un système d’écriture puissant. Avec l’objectif d’adresser des applications pour la muséographie, le problème consistait à faire évoluer le modèle linéaire du logiciel i-score vers un modèle comportant des conditions, à la fois de façon cohérente sur le plan théorique et satisfaisante en regard aux exigences des utilisateurs. La difficulté majeure de ce travail était due au fait qu’il n’existait pas d’exemples de cas pouvant être étudiés par les scientifiques, le concept étant complètement novateur. L’étude s’est alors construite sur les échanges entre les imaginaires des utilisateurs, des scientifiques et des ingénieurs.
1.2 De l’arbre au graphe
4Pour les besoins de la présentation de ce travail, nous utiliserons les notions d’arbres et de graphes que nous expliquons brièvement ici.
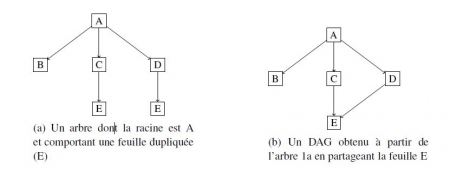
5Un arbre est une structure récursive composée d’un ensemble de nœuds, dont l’un d’entre eux est appelé la racine. On distingue 3 types de nœuds : 1) les nœuds internes contenant un ensemble de nœuds appelés enfants, et qui sont eux-mêmes qualifiés de parents ; 2) les feuilles, qui sont des nœuds sans enfants ; et 3) la racine, qui est un nœud sans parent. Dans un arbre, tout nœud différent de la racine a un et un seul parent. Quand cette propriété n’est pas vérifiée, nous avons affaire à un graphe. L’exemple qui va nous intéresser particulièrement est le passage d’un arbre à un graphe par le partage de nœuds. Sur la Figure 1a, on a représenté un arbre comportant deux feuilles étiquetées de façon identique (les feuilles étiquetées E) et qui sont enfants de deux parents différents (les nœuds C et D), et sur la Figure 1b, la feuille E de cet arbre est partagée entre les deux parents C et D. Cette feuille admettant alors deux parents, la structure n’est plus un arbre mais un graphe. Plus précisément, il s’agit un DAG (Directed Acyclic Graph) car ce type de graphe a la propriété de ne pas comporter de chemins rebouclant sur son origine, un chemin étant une suite de nœuds voisins, c’est-à-dire reliés par la relation hiérarchique de parenté.
Figure 1 : Un arbre et un DAG correspondant au partage de la feuille E entre les parents C et D
1.3 Scénario arborescent linéaire
6Un célèbre exemple de scénario non linéaire se trouve dans le film Smoking/No Smoking d’Alain Resnais qui raconte plusieurs versions d’une histoire. Le scénario est défini par un arbre binaire3 qui représente toutes les versions de l’histoire, chaque nœud contenant une scène et une bifurcation scénaristique représentée par deux enfants et chaque arc représentant la durée écoulée entre la scène parent et la scène enfant. Dans le film, ces versions sont présentées en enchaînant les scènes dans un ordre préfixe obtenu par un parcours en profondeur de l’arbre, et donc en effectuant des retours dans le passé à chaque remontée dans l’arbre. Donc au final, le scénario se présente linéairement.
1.4 Scénario arborescent multiple
7Cependant, notre problème consiste à produire, lors de l’exécution, une seule version qui se déroule dans le temps réel conformément aux relations temporelles définies dans le scénario, les bifurcations dépendant de données acquises lors de l’exécution. Une version du scénario correspond donc à un chemin dans l’arbre des versions allant de la racine vers une feuille. Un modèle mieux adapté à ce problème est celui de l’espace-temps de la physique théorique dans lequel toutes les configurations physiques naturelles sont superposées et dont l’évolution se décompose en plusieurs branches [DC]. Dans ce modèle, toutes les évolutions existent en même temps, chacune d’elles ayant sa propre amplitude d’existence, mais nous n’en percevons qu’une seule. L’exécution d’un tel modèle correspond plutôt à un parcours en largeur et en parallèle de l’arbre des histoires.
1.5 Scénario multiple non arborescent
8La nature arborescente du scénario pose un problème d’explosion combinatoire dès que le nombre de cas augmente ainsi qu’un risque de difficulté d’édition pour l’utilisateur. Le partage de parties communes entre plusieurs versions conduit à utiliser un graphe plutôt qu’un arbre (voir la sous-section 1.2). La concision de cette représentation évite la gestion de l’explosion combinatoire des cas dépliés par l’utilisateur ou le système. Par conséquent, cette mise en facteur procure un meilleur confort d’édition.
9Mais ce modèle est plus difficile à maîtriser par les utilisateurs car les différentes versions sont mélangées et partagent des événements. Par conséquent, le passé des événements est dynamique et peut poser des problèmes d’écriture (dans l’exemple 1b, le passé de E peut être soit C soit D). Cependant, la puissance d’expression est beaucoup plus intéressante car elle permet de travailler soit sur un arbre comme le modèle précédent, soit de créer des parties communes, et elle est compatible avec un modèle hiérarchique.
2 L’existant
10À l’origine, le projet disposait du logiciel i-score basé sur un modèle de scénario linéaire à temps souple dont l’exécution était assurée au moyen d’un réseau de Petri [Pet, 2066] à flux temporisé hiérarchique et coloré cadencé à la milliseconde [ADCA, 2008 ; ADCLA, 2008 ; ADCT, 2011] développé lors du projet ANR Virage [AMDC+2010]. Le scénario était linéaire mais la souplesse du temps permettait déjà d’avoir plusieurs versions temporelles du scénario.
2.1 Le modèle linéaire initial
11Un scénario linéaire est défini de façon hiérarchique. Il comprend les éléments suivants :
12• Un ensemble d’événements correspondant chacun à un début ou une fin de scénario (voir définition ci-après).
13• Des relations temporelles reliant deux événements :
-
ces deux événements sont dits respectivement l’événement source et l’événement but ;
-
ces relations sont des relations de précédence de points quantifiées par un intervalle de temps borné par des valeurs minimum et maximum ;
-
on appellera relations entrantes d’un événement les relations admettant cet événement pour but ;
-
une relation temporelle est dite souple si son intervalle de temps minimum est strictement plus petit que son intervalle de temps maximum.
14• Des sous-scénarios correspondant chacun à un couple formé d’une relation temporelle et d’un processus ou d’un scénario admettant pour début l’événement source et pour fin l’événement but de la relation.
15• Des points d’interaction permettant d’effectuer le déclenchement lors de l’exécution en temps réel de certains événements, ces événements étant donc datés au moment de l’exécution. Ces événements sont dits interactifs.
16Ces événements sont toujours utilisés comme buts d’une relation temporelle souple.
2.1.1 États des événements et des relations
17Pour les besoins du développement suivant, il est nécessaire d’introduire un peu de terminologie sur les états des éléments du langage de l’interface durant l’exécution d’un scénario.
18Une relation temporelle admet les états suivants :
19• active : son événement source a été déclenché et le temps écoulé depuis est inférieur à la borne minimale de son intervalle de temps ;
20• vérifiée : son événement source a été déclenché et le temps écoulé depuis appartient à son intervalle de temps ;
21• désactivée : son événement source a été déclenché et le temps écoulé depuis est supérieur strictement à la borne maximale de son intervalle de temps ;
22• inactive : en attente d’une activation.
23Un événement admet les états suivants :
24• déclenchable : ses relations entrantes sont toutes vérifiées ;
25• actif : l’événement est en cours de déclenchement ;
26• desactivé : l’événement a été déclenché ;
27• inactif : en attente d’une activation.
2.1.2 Ordre partiel des événements
28Les relations temporelles définissent un ordre partiel entre tous les événements, qu’ils soient interactifs ou non. Lors de l’exécution, cet ordre est respecté.
2.2 Les propositions théoriques d’évolution
29Une première étude de l’extension du modèle linéaire a été effectuée durant la thèse de Mauricio Toro et a conduit à des propositions de modèles logico-temporels définis formellement [TDC, 2011, TDCR, 2014].
2.2.1 Des relations temporelles aux relations logico-temporelles
30Une des propositions de cette thèse a consisté à étendre les relations temporelles du modèle linéaire à des relations logico-temporelles en ajoutant une condition booléenne sur chaque relation temporelle. Ainsi, pour qu’une relation logico-temporelle soit vérifiée, il faut que la condition soit vraie et que la contrainte temporelle soit vérifiée. Une relation logico-temporelle non vérifiée invalide son événement but, ainsi que la suite du scénario qui dépend de cet événement. Ce travail a conduit à l’élaboration d’une sémantique basée sur des graphes d’événements, les choix étant représentés par des conflits et utilisant la notion d’exécution silencieuse permettant d’attendre sans exécuter, prémisse de l’idée qui a conduit au modèle retenu. Par contre, aucun modèle opérationnel n’a été proposé.
2.2.2 Des scénarios linéaires aux scénarios conditionnels
31Un modèle alternatif basé plutôt sur la notion de scénario conditionnel a également été proposé. Ces scénarios conditionnels comportent des conditions exclusives à l’entrée ainsi que plusieurs sous-scénarios internes dont chacun correspond à un cas, à l’instar des clauses gardées ou de la forme « cond » du langage lisp. Ces scénarios conditionnels ont un point d’interaction sur leur événement de début qui reçoit, lors de son activation, un message permettant de déterminer le cas qui sera activé.
32Les sous-scénarios sont indépendants, au sens où il n’y a pas de relations temporelles entre deux événements situés dans deux sous-scénarios différents. L’utilisateur est assuré de construire des scénarios cohérents avec cette modélisation. Celle-ci lui permet de créer des sous-versions localement tout en conservant la possibilité de définir des parties communes à plusieurs versions, en dehors des structures. La sémantique du modèle, définie hiérarchiquement et donc algébriquement, en est simple, de même que le modèle opérationnel.
3 De l’arbre au graphe
3.1 Les échanges avec les utilisateurs
33Les échanges avec les utilisateurs du projet OSSIA ont bousculé les propositions théoriques et impliqué la recherche d’un nouveau modèle.
34La proposition de scénarios conditionnels a été rejetée pour des raisons de puissance d’expression. En effet, le modèle hiérarchique interdit de poser des relations entre des sous-scénarios différents, limitant ainsi l’expressivité du modèle, et imposant une pratique de copie alourdissant soit l’interaction utilisateur, soit l’interface du système.
35Le besoin de partage d’événements buts de plusieurs relations a été exprimé, dans un souci à la fois de puissance d’expression et de concision du scénario.
36C’est donc le modèle d’un arbre avec partages d’événements (un Directed Acyclic Graph) qui a été retenu par tous les participants du projet, un choix ambitieux et risqué. Il s’agit d’un graphe de relations pouvant relier n’importe quels événements comprenant : 1) des éléments les plus basiques possible et une liberté totale de construction, pour pouvoir explorer sans entraves ce nouveau terrain d’expérimentations, mais avec la prise de risque due à la difficulté, pour les utilisateurs, de maîtriser un modèle complexe et puissant ; 2) le problème de définir, pour les scientifiques, un modèle opérationnel simple, fiable et robuste pour l’exécution d’un scénario représenté par un graphe et ;3) la contrainte, pour les ingénieurs, de pouvoir faire évoluer le code existant de façon cohérente et fiable.
3.2 Les événements conditionnels
37Dans ce modèle, la notion de scénario conditionnel est remplacée par celle d’événement conditionnel.
38Un événement conditionnel est un nouvel objet dans le modèle qui va servir à construire les chemins des différentes versions. L’événement interactif conditionnel est isolé et ne correspond ni à un début ni à une fin de sous-scénario. Un événement conditionnel comporte plusieurs clauses gardées, qui sont évaluées en séquence dans le même tic d’horloge, lors du déclenchement de l’événement. Ces clauses comportent chacune une condition booléenne en prémisse et une ou plusieurs relations en conséquence. Ainsi, l’exécution d’une clause consiste à évaluer la condition puis à activer la ou les relations si celle-ci est vraie.
39Les utilisateurs ont souhaité que les clauses ne soient pas exclusives. Donc contrairement à la forme « cond » du langage lisp, toutes les clauses sont évaluées quels que soient les résultats des conditions. Ainsi, n’importe quelle configuration de déclenchements est permise.
3.3 Cas critiques de scénarios non linéaires
40Nous nous plaçons maintenant dans le cadre d’un scénario non linéaire avec partage d’événements buts de plusieurs relations correspondant à des cas différents. Ainsi, au moment de l’exécution, certaines relations entrantes de ces événements sont actives et d’autres non. La gestion du déclenchement de ces événements pose alors les questions suivantes : comment combiner l’attente de la vérification des relations temporelles entrantes de ces événements pour décider de leur déclenchement ? Faut-il utiliser une conjonction, comme dans le modèle précédent, une disjonction, ou bien faut-il imaginer un autre mécanisme ? Faut-il donner le choix à l’utilisateur ?
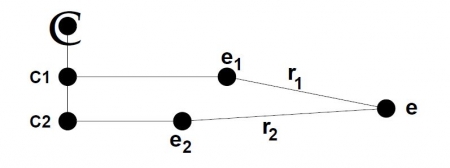
41Pour illustrer ce problème, prenons l’exemple suivant qui nous servira tout au long de cet article. Cet exemple est illustré sur la Figure 2. Soit un événement conditionnel portant deux conditions booléennes c1 et c2 indépendantes. On considère deux relations temporelles conséquences de ces deux clauses, l’une associée à c1 et allant vers un événement e1 et l’autre associée à c2 et allant vers un événement e2.
Figure 2 : Exemple de conditions dans un scénario non linéaire : les deux conditions c1 et c2 sont synchronisées sur un événement conditionnel. L’événement e est partagé par les deux chemins partant de c1 et c2
42Si l’utilisateur construit un événement e admettant r1 comme relation entrante provenant de e1, le déclenchement de e est conditionné par la vérification de la relation r1 et donc par le déclenchement en amont de e1, conformément au modèle initial. Mais si l’utilisateur construit en plus une relation temporelle r2 allant de e2 vers e, les questions suivantes se posent :
43• l’événement e doit-il attendre que r1 et r2 soient vérifiées ? auquel cas il s’agit d’un mécanisme de conjonction ;
44• l’événement e doit-il attendre la vérification de l’une des deux relations seulement ? auquel cas il s’agit d’un mécanisme de disjonction.
45Si plus de deux conditions sont considérées, les cas sont plus nombreux et difficiles à exprimer.
3.3.1 Scénario arborescent
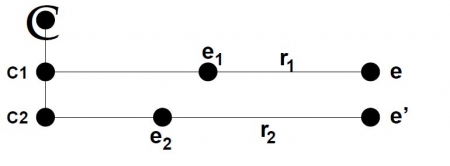
46Notre scénario étant un scénario arborescent avec partage d’événements, nous nous référons au scénario arborescent pour décider du bon fonctionnement de la combinaison des relations temporelles. Nous pensons ainsi mettre en œuvre un mécanisme suffisamment intuitif pour l’utilisateur. Ce scénario est illustré sur la figure 3 dans lequel l’événement e a été séparé en deux événements différents e et e’. Étant donné que le résultat des conditions c1 et c2 est imprédictible statiquement, tous les cas suivants peuvent se produire :
Figure 3 : Exemple de conditions dans un scénario arborescent : les deux conditions c1 et c2 sont synchronisées sur un événement conditionnel. L’événement e est séparé en deux événements e et e’
47• c1 est vraie et c2 est fausse : l’événement e1 sera déclenché, puis la relation r1 sera vérifiée et provoquera le déclenchement de e. Par contre, l’événement e2 ne sera pas déclenché, et en conséquence la relation r2 ne sera jamais vérifiée. Comme l’événement e’ attend la vérification de la relation r2, il ne s’activera jamais, bloquant ainsi toute la suite du scénario ;
48• c1 est fausse et c2 est vraie : cas symétrique ;
49• c1 est fausse et c2 est fausse : ni e ni e’ ne seront déclenchés ;
50• c1 est vraie et c2 est vraie : les deux événements e et e’ seront déclenchés lors de la vérification de leurs relations entrantes.
51Dans cet exemple arborescent les événements e et e’ ne sont pas synchronisés puisqu’aucune relation temporelle ne les relie. Par contre, dans le scénario avec partage que nous étudions, ces deux événements sont identifiés en un seul et sont donc synchronisés. Ainsi, la coïncidence de la vérification des relations r1 et r2 se posera en plus de la vérification des conditions logiques, ce qui posera un problème notamment dans le cas de la disjonction.
3.3.2 Conjonction : risques de blocages
52Examinons ce qui se passerait dans notre scénario avec partage si nous combinons les relations au moyen d’une conjonction. Dans le cas de la conjonction, le déclenchement de l’événement e se produit quand r1 et r2 sont vérifiées.
53• c1 est vraie et c2 est fausse : l’événement e2 ne sera pas déclenché, et en conséquence la relation r2 ne sera jamais vérifiée. Comme l’événement e attend la vérification de la relation r2, il ne s’activera jamais, bloquant ainsi toute la suite du scénario ;
54• c1 est fausse et c2 est vraie : même fonctionnement ;
55• c1 est fausse et c2 est fausse : l’événement e ne se déclenchera pas conformément au cas arborescent ;
56• c1 est vraie et c2 est vraie : les deux relations étant vérifiées, l’événement e se déclenchera conformément au cas arborescent.
57Les résultats divergent de celui du scénario arborescent dans les deux premiers cas. La conjonction ne permet donc pas de représenter correctement un partage d’événements buts.
3.3.3 Disjonction : risques d’exécutions multiples
58Dans le cas de la disjonction, une seule des relations peut déclencher e. Nous avons les cas suivants :
59• si l’une des conditions c1 ou c2 est vraie, un seul des événements e1 ou e2 et une seule des relations r1 ou r2 sont activés. L’événement sera déclenché lors de la vérification de la relation activée (soit r1 soit r2 selon le cas) ;
60• si les deux conditions sont vraies, les deux événements e1 et e2 sont déclenchés ainsi que les relations r1 et r2. Le résultat risque de dépendre de l’ordre dans lequel les relations r1 et r2 sont vérifiées. Si la première permet le déclenchement de e, la deuxième risque de déclencher e une deuxième fois en décalé, ou bien produire des erreurs si les processus ne sup- portent pas une deuxième exécution ;
61• si aucune des deux conditions n’est vraie, aucune des relations ne sera activée et l’événement e ne sera donc pas déclenché, conformément au cas arborescent.
62Le mécanisme de disjonction présente donc des risques d’exécutions multiples des parties de scénarios qui seraient partagées par plusieurs versions du scénario. En effet, des versions indépendantes actives peuvent déclencher plusieurs fois en séquence ces sous-parties comme dans l’exemple ci-dessus, puisqu’aucune synchronisation n’est effectuée sur l’événement e.
3.3.4 Choix utilisateur/choix système
63Aucun des deux mécanismes ne fonctionne parfaitement dans tous les cas. Il serait possible de donner le choix à l’utilisateur d’utiliser soit une conjonction soit une disjonction selon le cas qui l’intéresse. Mais compte tenu des risques de blocages ou d’exécutions multiples, une expertise importante de l’utilisateur est requise. Or, dans le projet OSSIA, l’utilisation du système doit être simple et intuitive et il est impératif de ne pas mettre l’utilisateur devant une telle responsabilité. La voie que nous avons adoptée consiste plutôt à faire un choix par défaut au niveau du système, quitte à réduire dans un premier temps l’expressivité du modèle pour que celui-ci évite les risques évoqués et puisse être facilement maîtrisé par l’utilisateur. Son implémentation a consisté à exploiter la couleur des jetons du réseau de Petri.
4 Le modèle retenu
64Basé sur la théorie des mondes multiples, le modèle retenu permet de relier de façon cohérente l’écriture et l’exécution du scénario car le modèle de temps décrit la dynamique de façon statique.
4.1 La théorie des mondes multiples
65Cette théorie issue de la physique théorique introduit l’indéterminisme dans l’espace-temps. Selon cette théorie, plusieurs mondes sont superposés, au sens quantique du terme. Chaque monde est composé de configurations physiques naturelles et de leur évolution. Chacune de ces évolutions appelée histoire possède une amplitude d’existence qui peut se concevoir comme une couleur. Deux particules sont de la même couleur, c’est-à-dire dans le même monde, si elles sont en interaction. Pour passer d’une configuration à une autre, toutes les couleurs de toutes les histoires sont mélangées. Ainsi, nous avons l’illusion d’une seule réalité, alors que plusieurs autres réalités se déroulent hors de notre propre monde [DC].
66Cette théorie constitue une excellente source d’inspiration pour faire évoluer notre modèle vers l’indéterminisme. En effet, elle est complètement compatible avec l’indéterminisme temporel déjà présent dans le modèle initial [DCAA, 2013] : tous les cas sont présents dans la partition, mais une seule version s’exécute.
4.2 Le modèle opérationnel
67Ce modèle consiste à considérer que toutes les versions d’un scénario s’exécutent en même temps avec des amplitudes d’existence propres. Comme dans la théorie physique des mondes multiples, tous les cas existent mais seuls ceux qui sont en interaction sont dans le même monde. Dans notre modèle, cela signifie que les événements reliés par une relation temporelle sont dans une même version. De plus, toutes les versions s’exécutent, mais une seule est perçue lors d’une exécution donnée. Les événements de la version perçue se voient attribuer une amplitude d’existence de 1 et les autres d’une amplitude de 0. Une exécution consiste donc à parcourir le graphe du scénario en propageant en temps réel les amplitudes d’existence en fonction des relations temporelles qui sont valides.
68L’implémentation du modèle initial est basée sur un réseau de Petri temporisé coloré et hiérarchique [JK09]. Le réseau étant donné en statique, seuls les jetons portent des informations dynamiques. L’idée de ce modèle est donc d’utiliser les couleurs des jetons pour porter les amplitudes d’existence.
69On obtient deux types de jetons :
70• les jetons actifs qui activent pleinement les événements et les relations temporelles ;
71• les jetons passifs qui ne font que passer sans déclencher les événements, ni exécuter les processus, ni attendre les intervalles de temps des relations temporelles.
72Ainsi toutes les réalités s’exécutent, mais seule la réalité perçue effectue pleinement les calculs.
4.3 Un nouvel état
73Il est nécessaire de considérer un nouvel état correspondant aux événements et relations traversés par des jetons passifs. Ainsi, on définit l’état invalide de la façon suivante :
74• une relation se trouvant dans une clause dont la condition est fausse est invalide ;
75• un événement n’ayant que des relations entrantes invalides est invalide ;
76• une relation ayant pour source un événement invalide est invalide ;
77• un événement ayant au moins une relation entrante vérifiée est déclenché ;
4.4 Une conjonction pour simuler une disjonction
78Avec un tel modèle d’exécution, les événements admettant plusieurs relations entrantes sont déclenchés lorsque toutes les relations actives sont vérifiées. Ce fonctionnement correspond à celui du scénario arborescent. En effet, il simule une disjonction dans la réalité perçue, puisque l’événement but sera activé dans tous les cas sauf si toutes ses relations entrantes sont invalidées.
79Ainsi, la conjonction opérationnelle lors de l’exécution apporte la synchronisation qui permet d’éviter le risque d’exécutions multiples. La disjonction perçue dans la réalité, pour sa part, permet de partager des parties du scénario sans se soucier de blocages éventuels pouvant être dus aux synchronisations avec des versions non actives.
4.5 Cas critiques
80Reprenons l’exemple précédent pour illustrer le comportement du système sur les cas critiques. Lors de l’exécution les cas suivants peuvent se produire :
811. les deux conditions c1 et c2 sont vraies : les deux événements e1 et e2 sont activés lors de la vérification de leurs relations temporelles entrantes. Puis e est activé lors de la vérification des relations r1 et r2, comme dans le modèle linéaire on a une véritable conjonction synchronisée ;
822. c1 est vraie et c2 est fausse : l’événement e1 est activé lors de la vérification de sa relation entrante, mais e2 est invalidé. La relation r2 s’en trouve invalidée et e est déclenché lorsque la relation r1 est vérifiée. La condition c1 suffit donc à déclencher e comme dans une disjonction et comme dans le cas du scénario arborescent ;
833. c1 est fausse et c2 est vraie : le cas symétrique marche tout aussi bien ;
844. c1 est fausse et c2 est fausse : les relations r1 et r2 sont invalidées, ce qui ne déclenchera pas e. L’événement e sera invalide sauf s’il a d’autres relations entrantes que r1 et r2 et que celles-ci sont valides.
854.5. Risques de blocages.
86Ce système permet d’éviter les blocages dus à des conditions fausses. En effet, les événements non activés sont traversés par des jetons passifs qui rejoignent les événements buts partagés, ce qui évite d’attendre les relations non activées. De plus, le système permet une édition fiable et incrémentale. Ajouter une relation temporelle vers un événement but n’apporte aucun risque de blocage quelle que soit la configuration du graphe.
4.5.2 Risques d’exécutions multiples
87Le problème des exécutions multiples se rapporte à la disjonction de relations temporelles ayant le même but et dont la vérification ne se produit pas en même temps. L’exécution multiple se produit si au moins deux relations sont vérifiées, ce qui implique deux activations en décalé de l’événement but.
88Dans notre modèle, le mécanisme de conjonction mis en place implique l’attente de la vérification de toutes les relations actives, ce qui nous prémunit d’un déclenchement précoce de l’événement. Les relations invalides étant traversées par des jetons qui ne prennent pas de temps, elles ne posent pas de problème d’attente.
4.5.3 Choix utilisateur/choix système
89Ce mécanisme ne nécessite aucun choix de la part de l’utilisateur. Le choix essentiel fait par le système est celui d’utiliser un mécanisme par défaut de conjonction simulant la disjonction qui évite complètement les problèmes de blocages et d’exécutions multiples. Cependant, l’expressivité du langage s’en trouve diminuée au profit de la fiabilité. Une véritable conjonction n’est pas exprimable dans ce modèle, mais comme indiqué en Perspectives, des solutions simples existent pour la mettre en place.
5 Perspectives
90Concernant l’expressivité du langage, il serait intéressant, dans des versions ultérieures, de mieux exploiter les amplitudes d’existence et de généraliser leur mélange. Dans le modèle actuel, un jeton actif suffit à déclencher un événement. On pourrait paramétrer ce comportement pour utiliser, par exemple, la somme des amplitudes d’existence, ce qui permettrait à l’utilisateur de définir combien de jetons doivent être reçus par un événement pour que celui-ci soit déclenché. On pourrait également exploiter la couleur des jetons, utiliser des amplitudes d’existence comprises entre 0 et 1 ou des nombres complexes, et paramétrer le seuil de perception des versions du scénario.
Conclusion
91Nous avons présenté une extension du modèle de scénario linéaire du logiciel i-score vers un modèle non linéaire en introduisant de la logique. Nous avons développé l’étude scientifique des propositions des utilisateurs et de leurs risques, et nous avons proposé un nouveau modèle permettant d’étendre simplement le modèle linéaire initial.
92Ce modèle est une des innovations majeures du projet OSSIA. Il a permis de répondre pleinement aux exigences des utilisateurs, tout en autorisant une évolution cohérente et simple du modèle. De plus, il allie puissance d’expression, fiabilité et simplicité d’utilisation. L’interface graphique permettant de manipuler ce modèle a été conçue, par la suite, par Pascal Baltazar, Théo de la Hogue et Blue Yeti.
93La pratique de ce logiciel et les nouveaux usages qui en découleront nous diront si celui-ci répond bien, en pratique, aux besoins du spectacle vivant et de la muséographie, mais également si ce modèle n’est pas trop complexe à maîtriser pour un utilisateur non-programmeur.
Bibliographie
[ADCA, 2008] Antoine Allombert, Myriam Desainte-Catherine and Gérard Assayag, Iscore, “Writing the Interaction” in Proceedings of the 3rd Digital Interactive Media in Entertainment and Art (DIMEA), Athens, September 2008.
[ADCLA, 2008] A. Allombert, M. Desainte-Catherine, J. Larraldeand G. Assayag, “A System of Interactive Scores Based on Qualitative and Quantitative Temporal Constraints” in Proceedings of ARTECH 2008 the Fourth International Conference on Digital Arts, Porto, 2008.
[ADCT, 2011] Antoine Allombert, Myriam Desainte-Catherine and Mauricio Toro (2011), “Modeling temporal constraints for a system of interactive score” in Constraint Programming in Music, p. 1-23. Wiley, 2011.
[AMDC+,2010] Antoine Allombert, Raphaël Marczak, Myriam Desainte-Catherine, Pascal Baltazar and Laurent Garnier, Virage: “Designing and Interactive Intermedia Sequencer from Users Requirements and the Background” in International Computer Music Conference, New York, June 2010.
[BdlHDC, 2014] P. Baltazar, T. de la Hogue and M. Desainte-Catherine, “I-score, an Interactive Sequencer for the Intermedia Arts”, in Workshop in Proceedings of Joined International Computer Music Conference and Sound and Music Computing (ICMC-SMC), Athena, 2014.
[DC] Thibault Damour and Jean-Claude Carrière, Entretiens sur la multitude du monde, Paris, Odile Jacob, date ????.
[DCAA, 2013] Myriam Desainte-Catherine, Antoine Allombert and Gérard Assayag,. Towards a Hybrid Temporal Paradigm for Musical Composition and Performance: The Case of Musical Interpretation. Computer Music Journal, 37(2):61-72, 2013.
[JK, 2009] Kurt Jansen and Lars Michael Kristensen, Coloured Petri Nets-Modelling and Validation of Concurrent Systems, Spring 2009.
[MDC, 2013] Pascal Baltazar et Théo de La Hogue Myriam Desainte-Catherine, Nicolas Hincker. Le séquenceur i-score. In Actes des Journées d’Informatique Musicale (JIM 2013), Saint-Denis, pages 159-160, 2013.
[Pet, 1966] Carl Adam Petri. Communication with Automata. PhD thesis, Universität Hamburg, 1966.
[TDC, 2011] Mauricio Toro and Myriam Desainte-Catherine. Concurrent constraint conditional branching interactive scores. In Sound and Music Computing (SMC)’10. Barcelona, Spain, pages 270-273, July 2011.
[TDCR, 2014] Mauricio Toro, Myriam Desainte-Catherine, and Camilo Rueda.
Formal semantics for interactive music scores: a framework to de- sign, specify properties and execute interactive scenarios. Journal of Mathematics and Music, Volume 8, Issue 1:93-112, 2014.
Notes
1 i-score.org
2 voir par exemple l’installation tumbleweed (son, lumière et fumée) des Baltazars, http://www.baltazars.org/project/tumbleweed/… et les installations de Renaud Rubiano et Nicolas Villenave lors du dernier festival Arts et Sciences de l’université de Bordeaux.
3 Voir par exemple http://nezumi.dumousseau.fr/film/smoking.htm