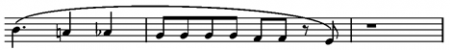Vers une modélisation combinatoire des structures rythmiques simples de la musique
David Janin septembre 2012
septembre 2012DOI : https://dx.doi.org/10.56698/rfim.222
Résumés
Résumé
Dans le domaine de la modélisation informatique des structures musicales, nous proposons ici une étude critique de la représentation informatique des motifs rythmiques simples qu’on peut rencontrer dans la musique occidentale du xviiie siècle à nos jours.
Notre approche se place dans la continuité des approches structuralistes incarnées, en particulier, par les travaux de Lerdahl et Jackendoff. Elle s’attache cependant plus spécifiquement à faire apparaître des opérateurs de composition et de transformation de motifs rythmiques. On souhaite ainsi pouvoir construire des motifs rythmiques complexes à partir de motifs rythmiques simples tout en rendant compte de la structure logique ou intentionnelle de ces motifs.
Cette perspective, plus combinatoire que les approches grammaticales classiques, nous conduit à distinguer pour chaque motif rythmique, sa réalisation : comment doit-il être joué ; de son usage : dans quel contexte peut-il être utilisé. Les structures informatiques qui en résultent, structures dans lesquelles les anacrouses et les conclusions deviennent explicites, peuvent ainsi être combinées séquentiellement tout en autorisant des superpositions partielles. En un certain sens, nous intégrons et généralisons ainsi, dans la description des motifs rythmiques eux-mêmes, la notion de métrique et des barres de mesures qui y sont associées. Le modèle obtenu peut alors contribuer à enrichir et à compléter les outils de composition existant. Il constitue en effet une extension conservative des systèmes de modélisations rythmiques utilisés dans des logiciels tels que Open Music.
La pertinence de notre proposition pour l’analyse ou la composition rythmique est évoquée à travers la modélisation de motifs rythmiques de plus en plus complexes.
Index
Index de mots-clés : modélisation rythmique et temporelle, modélisation des anacrouses, composition séquentielle et parallèle, recouvrement partiel, placement temporel vs placement causal.Texte intégral
1. Introduction
« La musique est le seul langage qui permette de comprendre plusieurs personnes qui parlent en même temps. »
1Ce clin d’œil du personnage d’Amadeus, dans le film éponyme de M. Forman, témoigne de la richesse historique du langage musical. Il faudra attendre plusieurs siècles et le développement des télécommunications modernes pour généraliser, en sciences et technologies, ce que les compositeurs maîtrisaient depuis longtemps : la communication multiplexée.
2Le langage musical est aussi, depuis des siècles, un langage de structuration du temps et de l’espace, un langage de description de comportements parallèles et interactifs. Son étude, sa modélisation formelle peut-elle conduire à de nouvelles métaphores, principes ou paradigmes utiles à la modélisation des systèmes informatiques modernes ?
3L’auteur, chercheur spécialisé dans les fondements théoriques des méthodes formelles pour la spécification, la modélisation et la vérification des systèmes informatisés, se propose de développer cette question en s’attachant, plus particulièrement, à l’étude et à la modélisation des structures rythmiques. La structuration du temps, complexe, en composition musicale comme en conception de systèmes informatiques, constitue sans doute l’un des piliers communs à ces deux domaines.
1. 1. Objectifs
4Dans cet article, nous tentons donc de développer un langage formel de description des structures rythmiques simples de la musique.
5A priori, ce langage doit être suffisamment riche et bien conçu pour permettre la construction simple et compositionnelle, d’un vocabulaire rythmique musicalement cohérent, qui intègre les notions rythmiques élémentaires de durées, métriques, phrasés, anacrouses, etc. Cette compositionnalité que nous visons est à comprendre au sens informatique. C’est-à-dire que chaque motif rythmique défini dans ce langage doit pouvoir être réutilisable, sans altération de ses propriétés principales, comme sous-composant de motifs plus complexes.
6Afin de faciliter la modélisation musicale, le langage visé doit aussi permettre la description syntaxique d’une intention rythmique trop souvent implicite, ou marginalement décrite, dans l’écriture traditionnelle de la musique. En particulier, ce langage doit pouvoir représenter l’articulation séquentielle ou parallèle de motifs rythmiques en veillant tout à la fois à leur positionnement causal, traduisant par exemple une écriture de question/réponse, leur positionnement temporel, il peut y avoir chevauchement entre plusieurs phrasés, notamment en présence d’anacrouses, leur mise en parallèle dans le cas de structures polyphoniques et/ou polyrythmiques, leur répétition, leur variation, etc.
1. 2. Quelques travaux et approches connexes
7Le travail présenté ici s’inscrit aussi dans la continuité de nombreux travaux de recherche en informatique théorique et en informatique musicale. Ils sont évoqués ci-dessous.
1. 2. 1. Une approche structuraliste
8Les propositions faites ici s’inscrivent sans nul doute dans la continuité des travaux de linguistique musicale formelle qui débutent, en particulier, avec (Lerdahl, Jackendoff, 1983) avec l’outillage conceptuel, structuraliste, offert par les grammaires génératives de Chomsky.
9Les développements modernes de l’informatique vers les systèmes parallèles et distribués bousculent cependant cette approche. Pour la représentation de la musique, intrinsèquement parallèle dans le cas de séquences polyphoniques ou polyrythmiques, avec des recouvrements partiels, il n’est pas forcément nécessaire de « séquentialiser » les structures musicales comme l’approche grammaticale semble le forcer. A priori, le formalisme des grammaires génératives, intrinsèquement liées à la modélisation arborescente, n’a pas vocation à représenter ce parallélisme.
10Dès la fin des années 1980, quelques auteurs proposent des langages de composition qui intègrent ce parallélisme. Desain et Honing (Desain, Honing, 1988) introduisent par exemple deux opérateurs : PRE et POST, qui permettent, comme nous allons le faire ici, de distinguer la définition d’un motif rythmique de son placement temporel. Ces opérateurs, présentés par les auteurs comme des opérateurs magiques et quelque peu adhoc, pour la programmation musicale, sont ici généralisés. Nous proposons en effet d’intégrer et d’expliciter dans nos modèles la distinction qu’ils induisent entre réalisation et synchronisation de motifs rythmiques.
1. 2. 2. Représentations informatiques vs représentations musicales
11Développer un formalisme de représentation de la musique pose aussi la question de savoir pour qui et pour quoi ce formalisme est développé. Ce peut être pour le compositeur ou bien pour l’interprète. Et chacun peut être un humain ou une machine.
12Pour la composition ou l’interprétation humaine, le langage musical est souvent chargé d’implicite. C’est en partageant une culture commune que le compositeur et l’interprète humain peuvent se comprendre mutuellement. Les notations musicales classiques sont par ailleurs très orientées lecture et interprétation. En particulier, les notations rythmiques, à travers les regroupements, les barres de mesure, etc., apparaissent souvent comme des repères visuels destinés aux interprètes pour se synchroniser de façon adéquate avec l’écoulement du temps physique.
13Au contraire, lors de l’interprétation d’une partition par ordinateur, dans ce cas la machine est interprète, ou bien lors de l’analyse automatisée d’une partition, dans ce cas l’ordinateur est un auditeur, cette « facilité » de lecture devient obsolète. Un ordinateur n’a aucune peine à compter les fractions de seconde. Par contre, en l’absence de contexte culturel, il devient nécessaire d’expliciter l’implicite musical. Ainsi, la métrique de la musique, avec les notions de temps forts et de temps faibles qu’elle induit, son phrasé, ses éléments stylistiques, sont autant de concepts qui doivent être explicitement modélisés pour se prêter à un traitement informatique.
14Visant indirectement à contribuer au développement d’un langage musical pour la composition et la performance musicale assistée par ordinateur, la réalisation de nos objectifs doit donc passer par une remise en cause de l’écriture musicale classique partiellement inadaptée à un usage informatique.
1. 2. 3. Dans la continuité de l’existant
15C’est cependant en partant d’une analyse de l’existant, aussi bien dans les notations traditionnelles que dans les notations plus informatiques déjà proposées, que nous cherchons à identifier les aspects sémantiques qui pourraient manquer ou être laissés à l’implicite culturel. Bien entendu, nous parlons ici de sémantique au sens informatique. Au sens opérationnel : comment la musique est-elle jouée ? Ou bien au sens structurel : comment la musique peut-elle être organisée ? En aucun cas nous ne cherchons à faire apparaître une quelconque notion (sans doute controversée) de sémantique musicale.
16Cette approche, qui pourra sans aucun doute sembler bien naïve à un musicien, cherche ainsi à produire un vocabulaire de composition et donc de représentation musicale qui soit tout à la fois le plus riche et le plus élémentaire possible. Idéalement, un tel vocabulaire rythmique devrait pouvoir coder, dans sa syntaxe même, tout un ensemble de constructions, de principes et d’opérateurs de haut niveau qui permettrait, ou tout du moins aiderait considérablement, un non musicien à écrire de la musique. Atteindre cet objectif signifiera sans doute que nous arrivons un peu plus à capturer, dans la syntaxe du langage proposé, cette compréhension profonde des structures musicales courantes que les musiciens partagent pour ainsi dire en initiés sinon en secret.
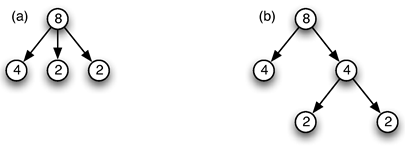
17Dans l’approche présentée ici, nous nous inspirons en particulier des travaux réalisés autour du logiciel OpenMusic et de la modélisation des structures rythmiques qui y est proposée (Agon et al., 1998 ; Bresson et al., 2009). Plus encore, les modèles définis ici constituent une extension conservative des modèles proposés par OpenMusic. Ces derniers apparaissent en effet comme des cas particuliers, facilement identifiables, des modèles proposés ici.
1. 2. 4. Une approche centrée sur la modélisation rythmique
18Dans cet article, nous nous concentrons sur ce qui pourrait constituer le grand oublié des travaux d’analyse musicale : l’analyse et la représentation des structures rythmiques indépendamment de l’analyse harmonique et mélodique.
19Bien sûr, il existe déjà des travaux sur l’analyse et la représentation des structures rythmiques (Toussaint, 2010). Mais la dynamique des phrasés rythmiques reste à ce jour beaucoup moins comprise que la dynamique des phrasés harmoniques ou mélodiques. Par exemple, le rythme harmonique produit par la tension provoquée par un accord de dominante qui se résout sur un accord de tonique, est aujourd’hui parfaitement intégré aux modèles musicaux. On peut y voir une dépendance causale : l’accord de dominante précède causalement l’accord de tonique. Il n’existe pas, à notre connaissance, de modèle formel, informatique, permettant de représenter des notions analogues de tensions et de résolutions purement rythmiques telles qu’on peut en trouver, par exemple, dans la musique romantique.
20Notre intuition est que, pour la modélisation musicale, l’analyse harmonique et mélodique a aujourd’hui atteint un tel degré d’avancement et de subtilité que toute avancée aussi minime soit-elle dans la compréhension et dans la représentation des structures rythmiques et de leurs articulations pourrait, en s’enrichissant des développements existants en harmonie et mélodie, conduire à des applications tout à fait conséquentes.
1. 2. 5. L’approche statistique
21Pour conclure ce parcours rapide de l’existant, mentionnons l’approche statistique, tout à fait orthogonale aux travaux initiés par Lerdahl et Jackendoff (Lerdahl, Jackendoff, 1983), qui est aujourd’hui développée avec succès.
22Ces méthodes s’appuient sur une analyse statistique de la musique (Pachet, 2002 ; Dubnov et al., 2003 ; Assayag et al., 2006 ; Assayag et al., 2007). Ainsi, elle ne présuppose pas, ou si peu, une compréhension a priori de la structure musicale. À partir d’un langage simple d’évènements musicaux et d’analyseurs statistiques performants, elle conduit cependant, a posteriori, à la mise au point d’algorithmes d’analyse et de restitution musicale spectaculaires. Dans ce cas, les statistiques permettent partiellement d’expliciter – à travers les modèles statistiques construits – la structuration implicite de la musique. Mais cela est fait sans vraiment faire apparaître les constructions qui pourraient expliciter cette structuration.
23Le succès de ces méthodes doit-il pour autant nous faire abandonner l’approche structuraliste que nous nous proposons de suivre ici ? Le pragmatisme conduit à répondre non. Ces deux approches peuvent sans aucun doute se nourrir et s’enrichir mutuellement.
24Le modèle proposé ici, qui conduit à une généralisation (Janin, 2012a) de la notion classique de mots, couramment utilisée dans la théorie des langages formels, pourra aussi et sans doute conduire à une extension de ces méthodes statistiques.
1. 3. Structure du rapport
25Dans la partie suivante, numérotée deuxième, nous étudions deux représentations bien connues de motifs rythmiques : la représentation arborescente en durée absolue et la représentation arborescente en durée relative. Nous obtenons ainsi une représentation arborescente classique, mixte, dans laquelle les sous-structures sont commodément décrites de façon relative. En cela, nous suivons les pas de la formalisation des structures rythmiques proposée, en particulier, par le logiciel OpenMusic (Agon et al., 1998).
26Ce modèle permet une représentation structurée des motifs rythmiques. À travers quelques exemples, nous passons en revue quelques-uns des arguments qui ont pu conduire à l’élaboration de ces formalismes. Ce questionnement, qui pourra sembler banal et bien connu au lecteur, nous permet cependant de mettre en évidence les faiblesses de cette modélisation. Cela nous conduira, dans les parties suivantes, à proposer un enrichissement de ce modèle. Cette partie, qui ne présente rien de nouveau, est essentiellement une introduction à la modélisation des structures rythmiques.
27Dans la troisième partie, nous nous attachons à décrire des structures rythmiques plus complexes qui font intervenir des constructions partiellement polyphoniques tel que le départ en anacruse. La combinaison séquentielle de ces structures rythmiques semble nécessiter d’autoriser des chevauchements temporels partiels. Ainsi, l’étude de ces exemples fait apparaître une carence du modèle présenté précédemment. D’une certaine façon, il manque à distinguer séquentialité causale et séquentialité temporelle. Par exemple, dans une écriture de questions/réponses rythmiques, un motif peut succéder causalement au motif qui le précède : il répond à ce motif, alors que le placement temporel de ces motifs fait apparaître des entrelacs et des superpositions partielles. Par exemple, une réponse peut démarrer avant la fin d’une question. En musique, une réponse peut même démarrer avant le début d’une question… Cela nous conduit, comme on le fait implicitement dans une partition polyphonique à l’aide des barres de mesure et des indications de métrique, à étendre la représentation arborescente des structures rythmiques par des points de synchronisation temporelle. On distingue ainsi la fenêtre temporelle d’un motif : la séquence totale de son exécution, de la fenêtre de synchronisation de ce même motif : la sous-séquence qui servira de repère de synchronisation avec les autres motifs. Cette approche, qui conduit à distinguer ordonnancement causal et ordonnancement temporel des motifs rythmiques, prend le contre-pied des approches à la Allen (Allen, Ferguson, 1997) qui ne traitent que de contraintes temporelles sur les intervalles de réalisation.
28L’originalité de notre proposition, s’il en est une, apparaît vraiment dans la quatrième partie. En nous appuyant sur la distinction faite entre réalisation temporelle et dépendance causale, nous proposons ce qui pourrait bien ressembler dans un premier temps à une astuce de codage de cette distinction. Plus précisément, nous proposons d’associer à tout motif rythmique un profil temporel qui décrit, à l’aide d’un triplet de valeurs, les durées relatives de l’introduction, du développement et de la conclusion du motif. Nous redéfinissons ainsi l’opérateur de composition séquentielle qui se prête bien mieux à la description et à la composition de motifs polyphoniques.
29Nous montrons ensuite, dans la cinquième partie, comment la composition séquentielle, combinée avec des opérateurs de resynchronisation, qui ne font que modifier le profil temporel de chaque motif en préservant sa fenêtre de réalisation, permet de définir plusieurs opérateurs dérivés de composition parallèle.
30Notre approche généralise les travaux de Desain et Honing (Desain, Honing, 1988) en ce sens que la pondération par triplet de durées, qui définit réalisation temporelle et synchronisation, se superpose, comme une sorte de calque, à la description du motif rythmique lui-même. Applicable dans un contexte plus large et plus souple, elle constitue donc une extension des opérateurs PRE et POST.
31Dans la sixième partie, l’astuce de codage proposée devient aussi une proposition de transformation des motifs rythmiques. En effet, en agissant sur le profil temporel d’un motif donné tout en préservant la durée de sa fenêtre de synchronisation, on obtient un nouvel opérateur d’expansion/contraction rythmique. Quelques exemples de motifs rythmiques présents dans les musiques populaires, du son cubain au rock’n’roll anglo-saxon, sont ainsi modélisés puis analysés. D’une certaine façon, nous définissons ainsi un opérateur de transformation rythmique permettant la description a priori d’une intention rythmique. Cette approche contraste avec les approches classiques, telles que celle de Toussaint (Toussaint, 2010), qui proposent des justifications a posteriori géométriques, des structures rythmiques.
2. Représentations arborescentes classiques
32Les structures arborescentes sont aujourd’hui couramment utilisées pour modéliser les structures rythmiques en musique (Bresson et al., 2009). Les langages de manipulation d’arbres, issues des mathématiques discrètes et de l’informatique théorique proposent alors tout un jeu d’opérateurs de transformation, de composition et de génération de structures rythmiques de plus en plus complexes qui peuvent trouver en musique une interprétation bienvenue. Les concepts associés à la manipulation d’arbres symboliques, déjà largement étudiés dans des contextes de recherche éloignés de l’informatique musicale, doivent pouvoir être adaptables à cette dernière.
2. 1. Durée absolue vs durée relative
33On peut modéliser toute structure rythmique élémentaire telle qu’une note ou un silence par un arbre à un seul sommet étiqueté par la durée de cette note ou de ce silence. Ensuite, ces atomes rythmiques peuvent être composés séquentiellement – ou concaténés – puis regroupés sous un nouveau nœud étiqueté par la somme des durées de ses successeurs. Ces nouveaux nœuds – et les sous-arbres étiquetés qu’ils induisent – représentent des structures rythmiques plus complexes qui peuvent elles-mêmes être concaténées et regroupées, etc. On peut ainsi engendrer des structures rythmiques de complexité arbitraire. Les durées des structures rythmiques modélisées étant codées dans un référentiel unique, on peut parler de représentation en durée absolue.
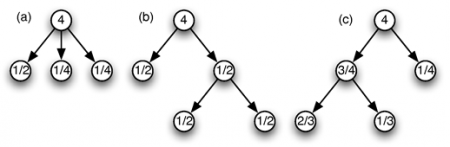
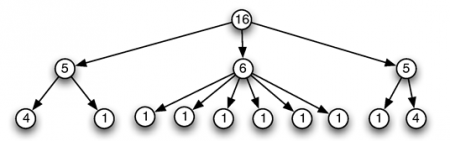
34Par exemple une blanche suivie de deux noires comme ci-dessous

35peut être représentée par l’un des arbres de la figure suivante :
36Dans cette modélisation, l’unité de durée est la croche.
37Dans le premier cas, la blanche et les deux noires sont représentées comme des éléments rythmiques de même niveau. Dans le second cas, les deux noires ont été regroupées en une sous-unité rythmique dont la durée globale est égale à la durée d’une blanche.
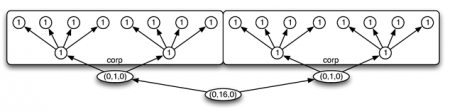
38La distinction syntaxique faite ici à travers ces deux représentations doit trouver une justification, sans doute, à la notion d’intention musicale. Par exemple, la seconde représentation semble donner une importance particulière à la première noire. En début de sous-structure rythmique, elle pourrait avoir un rôle particulier ; constituer par exemple un appui rythmique.
39Musicalement, cette distinction peut être modélisée comme suit :

40La représentation précédente s’appuie sur une représentation absolue des durées qui font référence à une unité de temps globale. Ces annotations de durées comportent cependant de la redondance. En effet, la durée des feuilles suffit à recalculer les durées de chacun des autres nœuds. En informatique, la redondance est à bannir. Combinée à des constructeurs et destructeurs de modèles d’information, la redondance est en effet potentiellement source d’incohérence et donc d’erreurs.
41Remarquons cependant qu’à partir de la durée globale et absolue de n’importe quelle structure rythmique, dès qu’on dispose des poids temporels relatifs de chacun des successeurs d’un même nœud, on peut tout aussi bien recalculer les durées absolues de chacun des nœuds. Il suffit en effet de répartir la durée globale de chaque nœud interne sur ses successeurs en respectant leur pondération.
42On peut ainsi coder l’exemple précédent de multiples façons. Nous donnons ici quelques instances de ces modélisations.
43En autorisant des poids réels positifs, les durées relatives des successeurs d’un même nœud peuvent même être normalisées de telle sorte que la somme des poids des successeurs d’un même nœud vaut 1. Il suffit en effet de diviser chacun des poids relatifs par cette somme. Dans l’exemple, les trois structures proposées le sont.
44La recherche d’une définition simple de produit séquentiel, dans lequel on ne souhaite pas rappeler les poids des motifs composés, nous conduit à adopter la convention suivante.
45Dans tous les modèles de structures rythmiques, le poids de la racine est absolu. Dans un référentiel temporel arbitraire mais fixe, le poids de la racine est uniquement déterminé par la durée globale du motif rythmique codé. Au contraire, le poids de tout nœud non racine est relatif. Les poids des nœuds non racine sont des durées relatives au poids des nœuds voisins c’est-à-dire des successeurs immédiats d’un même nœud.
46Bien entendu, dans tout le texte qui suit, la notion de durée manipulée est abstraite. Elle s’exprime dans une unité musicale telle que, par exemple, la croche, la noire ou la blanche.
2. 2. Interprétation de la structuration arborescente
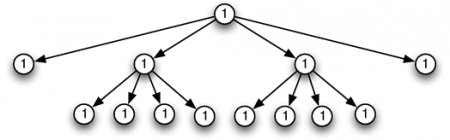
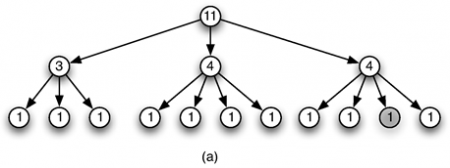
47Avant d’aller plus loin dans la construction de notre langage de manipulation rythmique, revenons un instant sur le sens à donner à cette structuration arborescente des motifs rythmiques. Quelle peut être sa sémantique ? Pour répondre, à cette question, prenons par exemple le motif suivant qui est composé de trois phrases musicales.

48Sur cette notation, on distingue deux types d’indication structurelle. Un premier regroupe les doubles croches en deux séries de quatre et permet de décomposer cette séquence en quatre paquets de longueur égale. Un second décompose, à l’aide de liaison, ce motif rythmique en trois phrases de longueur distincte.
49Le premier aspect peut être codé par la structure arborescente suivante :
50Dans ce codage, tous les nœuds qui apparaissent sont de même poids ce qui suggère que ce serait la notation la plus naturelle car la plus simple. Dans ce cas, très particulier, la pondération est même inutile. Bien entendu, ce n’est pas toujours le cas comme le montre l’exemple de la syncope. De plus, l’information de phrasé a disparu.
51Un second codage, proposé ci-dessous, rend compte de ce phrasé.
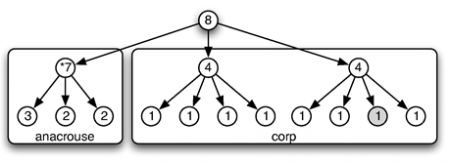
52Bien sûr, cette nouvelle structure semble bien plus difficile à lire. Il ne viendrait sans doute à l’idée d’aucun musicien de compter d’abord en 5, puis en 6 puis en 5 comme cette structure le suggère.
53Quelle sémantique faut-il privilégier ? Quel type d’indication structurelle présente dans la partition doit-on prioritairement intégrer dans notre formalisme ? Les notations musicales, développées empiriquement pendant des siècles, incorporent de nombreuses caractéristiques et aspects qu’il convient sans doute d’expliciter et de séparer dans une représentation structurée de la musique.
54Comme évoqué ci-dessus, les notations traditionnelles sont très orientées vers la lecture à vue ce qui est inutile pour une représentation informatique. Nous pourrons donc nous permettre de produire un codage structurel « illisible » des structures rythmiques dès lors que des modules de transcription adéquats pourront simplement et efficacement être utilisés pour en extraire des partitions lisibles par les musiciens. De nombreuses propositions, MusicXML ou Lilypond par exemple, sont aujourd’hui disponibles pour cela.
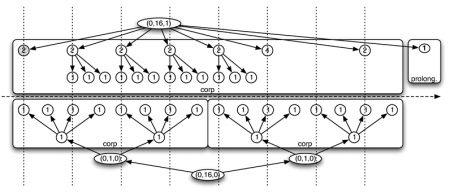
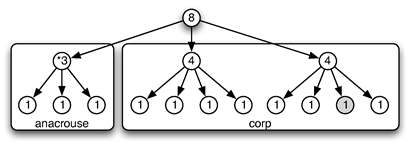
55Bien entendu, dans la plupart des exemples suivants, nous sacrifierons cependant à la lisibilité. Le lecteur n’est pas une machine. Ainsi, les représentations proposées seront souvent structurées à la manière des partitions.
2. 3. Un premier langage de construction rythmique
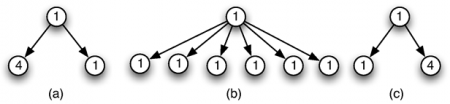
56Quels opérateurs de combinaisons de structures rythmiques sont disponibles sur ces modèles arborescents ? Pour répondre à cette question simple, considérons à nouveau l’exemple précédant, décomposé en trois phrases rythmiques :
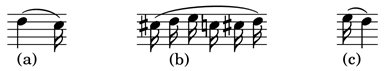
57Chacune de ces phrases peut être individuellement modélisée.
58La structure rythmique globale est alors facilement reconstruite à partir de ses composantes. Il suffit en effet de procéder à la composition séquentielle – ou concaténation – des structures rythmiques (a), (b) et (c) en les pondérant par 5, 6 et 5. On obtient, à nouveau, la structure suivante :
59À partir des éléments atomiques, composés séquentiellement, on obtient des éléments plus complexes qui peuvent à nouveau être composés les uns avec les autres… Formellement, on vient ici d’utiliser deux opérateurs sur les modèles arborescents de structures rythmiques.
60On utilise implicitement un opérateur de repondération. Pour tout motif rythmique m de durée d(m), pour chaque coefficient de repondération positif p>0, on définit le motif rythmique p.m obtenu à partir de m en prenant comme nouvelle durée absolue p.d(m). Insistons sur le fait que cette opération de repondération modifie uniformément la durée absolue de toutes les notes apparaissant dans le motif. En effet, dans ce modèle et dans tous les modèles suivants, la durée de chaque note apparaissant dans un motif est définie comme une certaine fraction, déterminée par la structure du motif, de la durée absolue du motif lui-même. Par exemple, étant donné le motif m composé de deux noires, le motif 2.m représentera deux blanches.
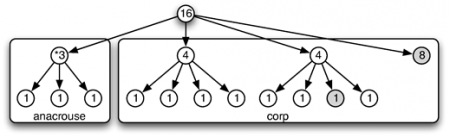
61On utilise aussi une version arborescente de la concaténation ou composition séquentielle. Pour toute séquence finie de k motifs rythmiques m1, m2, …, mk, on définit le produit de concaténation de ces k motifs comme étant le motif rythmique m obtenu par ajout d’une racine de durée
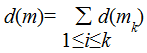
62et dont les sous-arbres sont définis comme étant, dans l’ordre, les (arbres codant les) motifs rythmiques m1, m2, …, mk.
63Bien sûr, ce deuxième opérateur n’est pas à proprement parler un opérateur de concaténation au sens usuel sur les mots. Cependant, en projetant chaque structure arborescente sur la séquence de ses nœuds feuilles, pondérés en durées absolues : le mot de feuilles induit par chaque structure, on constate que l’opérateur proposé ici agit bien comme une concaténation de mots au sens usuel.
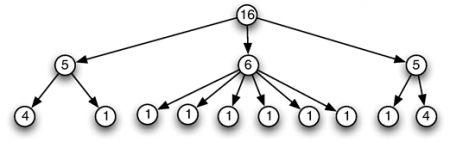
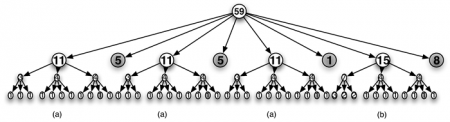
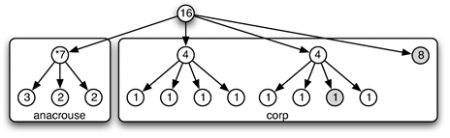
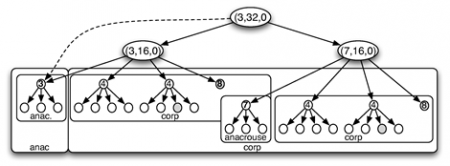
64Le langage de représentation des structures rythmiques ainsi défini est couramment utilisé dans les langages de composition. Il peut même être enrichi par d’autres opérateurs. La représentation arborescente proposée ici et l’algèbre qu’elle induit est-elle satisfaisante ? Nous nous proposons dans la partie suivante d’examiner quelques exemples de composition séquentielle de motifs rythmiques qui semblent la mettre en défaut. Cela nous conduira à l’enrichir de la notion de profil temporel.
3. Séquence logique vs séquence temporelle
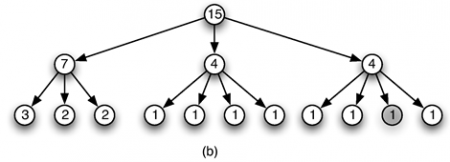
65Jusqu’à présent, nous avons soigneusement évité dans nos exemples de faire apparaître des métriques rythmiques. Nos exemples étaient-ils extraits de mesure à trois ou quatre temps ? Commençaient-ils sur des temps forts, des temps faibles ?
66Nous nous concentrons ici sur l’un des aspects sémantiques des signatures rythmiques : les indications de synchronisations temporelles qu’elles induisent. Plus précisément, l’indication de signature rythmique sur une partition et la position des barres de mesures qu’elle induit, apparaît en particulier comme un moyen de synchroniser plusieurs voix. Elle induit une notion de synchronisation par rendez-vous datés. Comment prendre en compte ces indications de synchronisation ?
67Observons qu’en informatique, on considère rarement ce type de rendez-vous à une date ou une succession de dates données. On rencontre en général des synchronisations par évènements telle que, par exemple, la réception d’un certain message sur un port donné. La musique pulsée appelle pourtant ce type de synchronisation sur le « temps qui passe ».
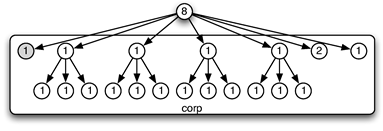
3. 1. Le problème de l’anacrouse
68Certaines structures rythmiques, couramment utilisées en musique, présentent la particularité de démarrer avant le premier temps d’un morceau. Plus généralement, une structure rythmique peut débuter avant le premier temps fort du motif qu’elle décrit. Ces départs par anticipation, ou anacrouse, conduisent à distinguer le premier évènement d’un motif : son début réel, du premier temps fort, son début logique.
69Une musique particulièrement riche en anacrouse est le Jazz Bebop. Nous nous proposons donc d’analyser puis de coder cet extrait du thème My little blue suede shoes de Charlie Parker.
70L’analyse élémentaire de cet extrait montre qu’il se compose de trois fois le même motif rythmique avant de se conclure sur une variation de ce même motif.
71Avec les notations précédentes, en grisant les soupirs pour les distinguer des notes jouées, le premier motif peut être représenté de la façon suivante :
72Le second motif peut, en suivant les mêmes conventions, être représenté de la façon suivante :
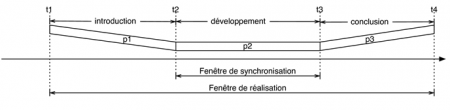
73Pour produire la séquence complète il nous suffit alors de concaténer en séquence trois fois le premier motif – noté (a) – puis une fois le second – noté (b) – en insérant les silences adéquats et en veillant tout particulièrement à mettre les bonnes pondérations.
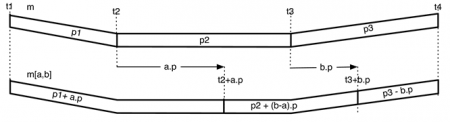
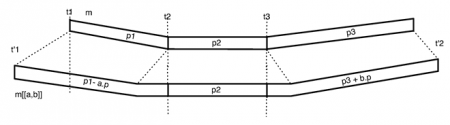
74La structure obtenue est la suivante :
75Que dire de cette représentation ? Remarquons tout d’abord que les motifs rythmiques (a) et (b) sont respectivement pondérés par 11 et 15 : leurs durées absolues, et les silences insérés sont respectivement pondérés par 5, 5, 1 et 8. À l’évidence, aucun musicien ou compositeur ne comptera ainsi.
76De plus, on ne retrouve pas dans ce modèle l’analyse, pourtant simple, qu’on a faite ci-dessus : trois expositions d’un premier motif puis l’exposition d’une variation sur le premier motif.
77Que d’encre gaspillée pourrait penser le musicien ! L’origine de cette complexité inutile est évidente : les barres de mesures ne sont pas encodées dans ces représentations ! Le musicien de Jazz peut même préciser : le début logique du motif est bien le premier temps de la première mesure, l’anacrouse ne compte pas. Mais comment modéliser de telles évidences musicales ?
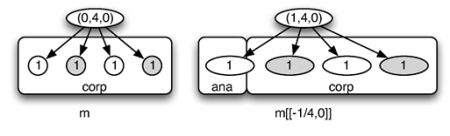
3. 2. Modélisation des anticipations
78En suivant les remarques de notre musicien imaginaire, modélisons explicitement le fait qu’une anacrouse commence avant le début logique d’un motif rythmique. Convenons par exemple de modéliser – temporairement – la distinction entre l’anacrouse et le corps d’un motif rythmique en faisant apparaitre le signe ’*’ devant les poids des éléments constituant l’anacrouse.
79Avec cette convention, le premier motif rythmique (a) de My little blue suede shoes peut être représenté, de la façon suivante :
80Le second motif rythmique (b) de ce thème peut, de la même façon, être codé comme suit :
81Pour la construction de la séquence rythmique totale, il semble cependant plus astucieux d’incorporer à ces séquences une mesure entière de silence de la façon suivante. Ainsi, pour le premier motif (a) on retient plutôt le codage suivant :
82qui code la séquence rythmique

83De la même façon, pour le second motif (b) on obtient :
84qui code la séquence rythmique
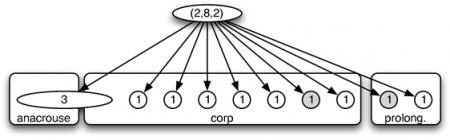
85Avec ce codage, l’ensemble de la phrase rythmique est obtenue par concaténation séquentielle de trois fois le premier motif plus une fois le second. Les corps de ces motifs sont positionnés, en séquence, les uns à la suite des autres. Les anacrouses se positionnent automatiquement en anticipation des corps des motifs rythmiques qui leur sont associés. On obtient ainsi le schéma suivant :
86Remarquons qu’on retrouve ici la structure logique en trois fois (a) plus (b). Les pondérations relatives de chacun des motifs sont simplifiées. Elles sont égales.
87Notons aussi que dans cette représentation de composition séquentielle, l’avancement du temps n’est vraiment effectif que dans les corps des motifs rythmiques. Les deux corps se succèdent temporellement l’un à l’autre. Les anacrouses ne viennent qu’en anticipation des corps rythmiques qu’elles précèdent, comme des éléments contextuels venant enrichir la réalisation d’une séquentialité logique. En particulier, toutes les anacrouses intermédiaires ne changent pas la durée globale du motif joué.
88Pour mieux comprendre la structure de l’arbre obtenu, reprenons un instant la dernière composition séquentielle. La structure suivante représente les quatre dernières mesures (et l’anacrouse correspondante) de notre extrait musical.
89Dans cette composition, nous obtenons un motif musical d’une longueur absolue de 35 croches. Mais la structure résultante ne compte réellement que 32 croches dans son corps rythmique. Elle admet une anacrouse de 3 croches qui est en quelque sorte héritée du premier motif de la composition.
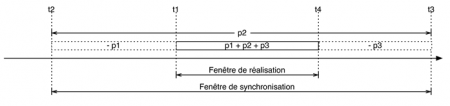
3. 3. Modélisation des prolongations
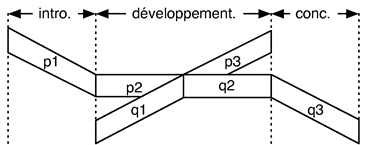
90La modélisation intuitive proposée ci-dessus s’applique aussi à la modélisation d’une notion symétrique à l’anacrouse : la prolongation. Une prolongation se compose d’une séquence de notes jouée après la fin logique d’un motif rythmique.
91Prenons par exemple la main droite des mesures 6 à 9 de la 1re Arabesque de Claude Debussy.
92Nous avons ici deux motifs rythmiques quasiment identiques, le premier semblant être égal au second augmenté d’une prolongation.
93Fort de l’étude déjà faite sur les anticipations, en distinguant les éléments d’une prolongation par le signe ’*’, nous obtenons, la durée absolue étant codée à la noire, le codage suivant de la première structure :
94et le codage suivant de la seconde :
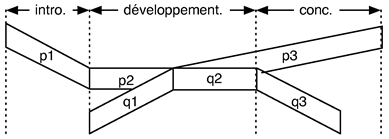
95Une simple concaténation produit alors la phrase tout entière :
96Le motif résultant n’a pas de prolongation. Là encore, la définition des prolongations permet de pondérer les deux motifs d’un même poids puisqu’ils ont des corps de même durée.
97Les notations graphiques utilisées jusqu’ici coïncident avec les opérateurs PRE et POST proposés par Desain et Honing (Desain, Honing, 1988). Ces opérateurs peuvent sembler adhoc. Nous proposons dans la partie suivante un codage bien plus systématique.
98Remarquons qu’avec les prolongations comme avec les anticipations, le temps n’avance réellement qu’avec le corps des motifs rythmiques. La prolongation de l’exemple ci-dessus est comme absorbée par le corps du motif suivant. En un certain sens, les prolongations comme les anticipations sont des éléments de contextes de réalisation indépendant de la structure logique du motif résultant de la composition.
4. Modélisation par triplets de durées
99De la partie précédente, nous concluons qu’un motif rythmique se modélise de façon pertinente à l’aide d’une introduction : une anacrouse ou anticipation, d’un développement : un corps, et une conclusion : une prolongation. À y regarder de plus près, cette modélisation ne fait que positionner, sur un motif rythmique complet, un instant logique de début et un instant logique de fin. Pour tout motif, ces notions ne permettent finalement que de distinguer une fenêtre de réalisation : le motif lui-même d’une fenêtre de synchronisation : son développement. Ce constat nous conduit à associer, à chaque motif rythmique, un profil temporel qui décrit cette distinction. L’opérateur de composition séquentiel peut alors être redéfini en s’appuyant sur ces profils temporels.
4. 1. Profil temporel d’un motif
100La distinction entre fenêtre de réalisation et fenêtre de synchronisation est réalisée par le typage (au sens informatique), de chaque motif m, par un profil temporel m(W)=(p1,p2,p3), où p1, p2 et p3 désignent respectivement les durées (ou poids relatifs) de l’introduction, du développement et de la conclusion du motif m.
101Cette notion de profil temporel est illustrée par le schéma suivant :
102En notant t1, t2, t3 et t4, les dates de début d’anacrouse, début de corps, début de prolongation et terminaison du motif rythmique. L’intervalle [t1,t3] définit la fenêtre temporelle de réalisation de la figure rythmique. L’intervalle [t2,t3] définit la fenêtre temporelle de synchronisation de la figure rythmique. Le respect des durées relatives de chacun des composants du motifs rythmique se traduit par les contraintes : (t2–t1)*p2=(t3–t2)*p1 et (t4–t3)*p2=(t3–t2)*p3.
103Ainsi, dès lors que la fenêtre de synchronisation est déterminée, c’est-à-dire que les dates t2 et t3 sont fixées, les dates t1 et t4 se déduisent des rapports de durées entre corps et anacrouse, et entre corps et prolongation, fixant ainsi la fenêtre de réalisation. Si les durées indiquées dans le profil temporel sont absolues, la donnée d’une seule de ces dates fixera les trois autres.
104Remarquons qu’un motif m, sans anacrouse ni prolongation, pondéré par une durée p, peut être pondéré par le profil temporel W(m) =(0,p,0). Autrement dit, cette modélisation des anticipation et prolongation par profil temporel est compatible avec la modélisation par durée relative évoquée dans la première partie. Comme annoncée, elle constitue donc bien une extension conservative de la modélisation arborescente des structures rythmiques en durées relatives telle que proposée dans le logiciel OpenMusic (Agon et al., 1998).
105Dans l’exemple évoqué ci-dessus, pour le motif m de profil temporel W(m)=(p1,p2,p3), on a 0<p1, 0<p2 et 0<p3. Ces conditions sont-elles nécessaires ?
106Il apparaît que, quitte à compléter par des silences la fenêtre de synchronisation, on peut aussi donner du sens à des motifs avec introduction et/ou conclusion de « durées » négatives.
107En effet, les calculs des dates t1, t2, t3 et t4 peuvent maintenant être pris comme des définitions. Ainsi, en particulier, lorsque p1<0 et p3<0, on obtient un motif avec une fenêtre de réalisation inclue dans la fenêtre de synchronisation.
108Un tel motif est illustré par le schéma suivant.
109Autrement dit, on convient d’autoriser tous les profils temporels de la forme (p1,p2,p3)ϵlR×lR×lR dès lors que p2<0, i. e. la fenêtre de synchronisation est de durée positive ou nulle, et p1+p2+p3<0, i. e. la fenêtre de réalisation est, elle-aussi, de durée positive ou nulle.
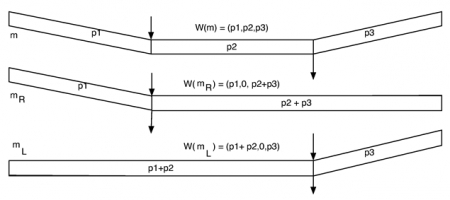
110Par convention, la durée du motif lui-même devant être codée à la racine de motif, nous faisons, comme précédemment, l’hypothèse de modélisation suivante. Dans toute structure rythmique, les pondérations par triplets de durées sont absolues à la racine et relatives sur les autres nœuds. Dans tous les cas, le poids relatif d’un sous-nœud par rapport aux nœuds voisins est défini comme la durée (relative) de son développement ou corps. Les durées relatives de son introduction et de sa conclusion sont ensuite modélisées relativement à la durée du développement ou corps du motif.
4. 2. Un exemple
111Cette pondération par triplet de durées a un avantage sur la modélisation évoquée précédemment. Elle est définie indépendamment de la structure rythmique du motif sur lequel elle s’applique. Ainsi, nous pouvons modéliser des anacrouses et des prolongations qui ne correspondent à aucun découpage structurel du rythme.
112Pour illustrer cette dernière propriété, observons le motif suivant qui pourrait être un motif rythmique d’improvisation en Bebop.

113D’un point de vue logique, la fenêtre de synchronisation – ou le corps –de ce motif est constituée de la mesure centrale. Il contient donc une anacrouse liée au premier temps de la fenêtre de synchronisation.
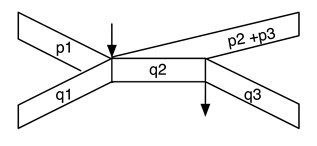
114Avec notre triplet de pondérations, ce motif de Bebop se code simplement par la structure pondérée suivante :
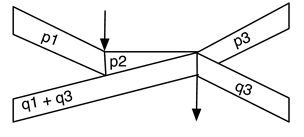
115Dans ce cas, la première noire pointée est en quelque sorte distribuée entre l’anacrouse et le corps du motif. Seul le nœud racine a vraiment besoin d’être pondéré d’un triplet non trivial, toutes les autres pondérations étant de la forme (0,p,0).
116Dans cet exemple, on comprend que la notion de structure temporelle d’un motif rythmique peut apparaître comme une transposition, en informatique, des notions de métrique et de mesures communément utilisées dans les notations musicales. En un sens, le profil temporel W(m) d’un motif rythmique m est une sorte de calque temporel, positionné sur le motif, qui indique comment ce motif doit être synchronisé avec les motifs alentours. Cette intuition devient explicite à travers la définition de composition séquentielle.
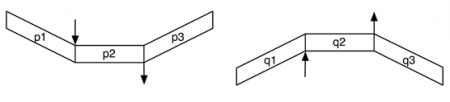
4. 3. Composition séquentielle revisitée
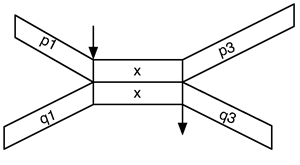
117La composition séquentielle de deux motifs avec anacrouse et prolongation est maintenant facile à définir. Il s’agit uniquement de faire coïncider, dans le temps, l’instant de fin du corps du premier motif avec l’instant de début du corps du second. Les anticipations et prolongations des motifs se placent alors en conséquence, générant l’anticipation et la prolongation du motif résultant.
118Formellement, étant donné un motif de profil temporel (p1,p2,p3) et un motif de profil temporel (q1,q2,q3), respectivement dessinés comme suit,
119on définit la composition séquentielle – notée d’un point – de ces deux motifs comme étant le motif obtenu par mise en séquence des corps des deux motifs avec pour profil temporel résultant :
120 (p1,p2,p3) (q1,q2,q3)=(max(p1,q1–p2),p2+q2,max(q3,p3–q2))
121et qui peut être dessiné comme suit :
122Dans le cas simple dessiné ci-dessus, on a q1<p1+p2 et p3<q2+q3. L’anacrouse du premier motif et la prolongation du second deviennent naturellement l’anacrouse et la prolongation du motif résultant de la composition séquentielle et la formule ci-dessus se simplifie en (p1,p2,p3) (q1,q2,q3)=( p1,p2+ q2,q3).
123La formule générale, plus complexe, proposée ci-dessus permet d’inclure le cas q1>p1+p2 : l’anacrouse du second motif commence avant l’anacrouse du premier motif, et le cas p3>q2+q3 : la prolongation du premier motif termine après la prolongation du second. Un tel exemple est illustré par le schéma suivant :
124L’extension de la composition séquentielle à des profils temporels avec anacrouses et/ou conclusions de durées négatives ne pose pas de difficulté particulière. Dans tous les cas, les fenêtres de synchronisation sont positionnées en séquences, la position des fenêtres de réalisation dérivant alors de ces positions.
125Pour notre exemple de Bebop, avec ces notations de profils temporels, la composition des quatre dernières mesures devient :
126Dans cette figure, comme évoqué ci-dessus, les pondérations (ou durées relatives) de la forme (0,p,0) ont été simplement notées p.
127Le lecteur curieux pourra vérifier que le produit ainsi défini sur les profils temporels est associatif et qu’il admet un élément neutre. La structure mathématique sous jacente est donc une structure de monoïde. Ce type de monoïde, appelé monoïde quasi-inversif, a récemment fait l’objet d’études spécifiques, dans le cas discret (Janin, 2012a) et dans le cas abstrait (Janin, 2012b). Ces études témoignent d’une richesse mathématique insoupçonnée, dans la prolongation de la théorie des monoïdes inversifs (Lawson, 1998).
5. Resynchronisation et opérateurs dérivés
128Nous avons vu dans la partie précédente comment modéliser à l’aide de profils temporels la distinction entre introduction, développement et conclusion de tout motif rythmique. Cette approche conduit à redéfinir le produit séquentiel qui, avec les profils temporels, permet la modélisation formelle des entrelacs et des superpositions musicales visés.
129Peut-on maintenant agir directement sur le profil temporel d’un motif ? Quel sens musical cela peut-il avoir ? Quels opérateurs de modélisation peuvent être dérivés de telles manipulations ? C’est ce que nous nous proposons d’étudier dans cette section.
5. 1. Resynchronisation
130Étant donné un motif rythmique m de triplet de durées (p1,p2,p3), étant donnée p=p1+p2+p3 la durée absolue de la réalisation du motif m, on peut envisager de déplacer la position de l’intervalle de synchronisation vis-à-vis de l’intervalle de réalisation sans changer la réalisation elle-même.
131En effet, étant donné deux offsets a en b, on définit m[a,b], la resynchronisation de m par un facteur a à gauche et b à droite, comme étant le motif dont la réalisation est identique à m mais dont le profil temporel est devenu W(m[a,b])=(p1+a.p,p2+(b–a).p,p3–b.p)
132Cette construction est illustrée par le schéma suivant :
133La somme des durées étant préservée par resynchronisation, cette opération ne fait vraiment que déplacer les points de synchronisation du motif sur lequel elle est appliquée.
134Appliquée aux notations musicales, la resynchronisation est illustrée par l’exemple suivant. Soit m le motif rythmique
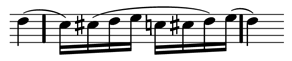
135de profil temporel W(m) =(1,2,1) qui code, à la noire, la position des barres de mesure. On peut générer le motif m[1,1] qui code le motif rythmique
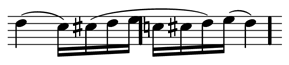
136de profil temporel W(m[1,1]) =(2,2,0). Dans ce cas, les facteurs de resynchronisation gauche et droit sont identiques. La resynchronisation n’a fait que translater la fenêtre de synchronisation d’une noire vers la droite.
137D’un point de vue musical, remarquons qu’une telle transformation est loin d’être anodine. La translation de la fenêtre de synchronisation d’une noire vers la droite modifie, dans cet exemple, la position des notes jouées vis-à-vis des temps forts et des temps faibles définis par la métrique sous-jacente. Dans une approche tonale, une telle transformation peut donc induire jusqu’à une modification du contexte harmonique. Cette remarque suggère que la distinction que nous faisons ici entre fenêtre de synchronisation et fenêtre de réalisation va potentiellement bien au delà d’une modélisation « de confort » pour la construction de motif complexe.
138D’un point de vue technique, remarquons aussi que l’opération de resynchronisation n’est que partiellement définie. A priori, à partir d’un motif m de profil temporel W(m)=(p1,p2,p3), la resynchronisation m[a,b] n’a de sens que lorsque la fenêtre de synchronisation obtenue est de taille positive ou nulle. Autrement dit, on doit avoir p2+(b–a).(p1+p2+p3)>0, c’est-à-dire,
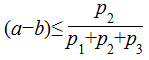
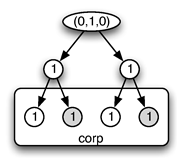
139Le cas d’égalité, étudié dans la partie suivante, se révèle particulièrement intéressant pour la modélisation.
5. 2. Motifs contextuels et opérateurs dérivés
140Un cas particulier de resynchronisation consiste à produire des motifs de fenêtres de synchronisation nulles. Les motifs obtenus, appelés motifs contextuels, ont la particularité de commuter lors d’une composition séquentielle, i. e. lorsque m et n sont deux motifs contextuels, m.n =n.m. En effet, leurs fenêtres de synchronisation étant de durée nulle, ils n’induisent aucun avancement du temps lors de la composition. Ils commutent donc.
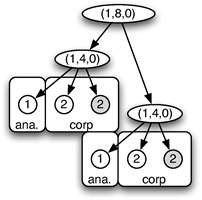
141Nous montrons de plus que, combiné avec la composition séquentielle, une notion de motifs contextuels canoniques associés à chaque motif permet de coder plusieurs produits parallèles.
142Plus précisément, à partir d’un motif m de profil temporel W(m)=(p1,p2,p3), la fenêtre de synchronisation du motif m[a,b] est nulle lorsque
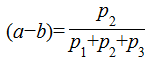
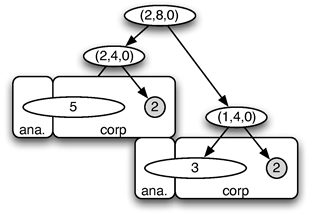
143Lorsque a =0, le motif obtenu, noté mr, est appelé contexte droit associé à m. Lorsque b =0, le motif obtenu, noté ml, est appelé contexte gauche associé à m. Ces deux contextes particuliers associés à tout motif sont illustrés dans le schéma suivant. Pour chacun des motifs, une flèche entrante et une flèche sortante marquent, respectivement, le début et la fin de chaque fenêtre de synchronisation.
144Muni de ces opérateurs de contexte, pour tous motifs rythmiques m et n, avec W(m)=(p1,p2,p3) et W(n)=(q1,q2,q3)
145on peut considérer le produit mr.n, appelé « fork », illustré par :
146et le produit m.nl, appelé « join », illustré par :
147qui code respectivement la synchronisation des motifs m et n sur le début de leur fenêtre de synchronisation pour le fork (dans ce cas la fenêtre de synchronisation résultante est héritée de n) et la fin de leur fenêtre de synchronisation pour le join (dans ce cas la fenêtre de synchronisation résultante est héritée de m).
148Lorsque m et n ont des fenêtres de synchronisation de même durée, on constate que ces deux produits coïncident en une sorte de composition parallèle de m et n. Plus précisément, tout se passe comme si l’on jouait ces deux motifs en les synchronisant maintenant sur leurs instants de début et sur leurs instants de fin. Les anacrouses et prolongations de chacun des motifs se disposent en fonction de la position du corps unique résultant.
149Formellement, à partir de deux motifs rythmiques m et n de profils temporels W(m)=(p1,x,p3) et W(n)=(q1,x,q3) on peut définir la composition parallèle de ces deux motifs comme étant le motif obtenu par juxtaposition des corps des deux motifs avec comme profil temporel résultant : (p1,x,p3)||(q1,x,q3)=(max(p1,q1),x,max(p3,q3))
150les anticipations et prolongations se disposant autour de ces corps. Cette composition parallèle peut être dessinée comme suit :
151Bien entendu, le max est utilisé dans la formule ci-dessus afin de calculer la durée de l’anticipation et de la prolongation résultante de ce produit. On vérifie que l’on a bien m||n=mr.n=m.nl=nr.m=n.ml, i. e. dans le cas de corps de même durée, non seulement « fork » et « join » coïncident, mais ils deviennent aussi commutatifs.
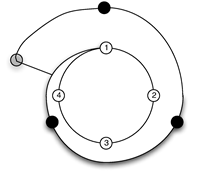
5. 3. Exemple de compositions multiples
152Pour illustrer ces constructions, considérons les deux mains des mêmes mesures 6 à 9 de la 1re Arabesque de Debussy.
153Nous avons déjà vu le codage de la main droite que nous rappelons ici pour les deux premières mesures avec la notation en triplets de durées :
154La main gauche sur les deux premières mesures, composée séquentiellement de deux motifs rythmiques identiques, peut être modélisée de la façon suivante :
155La composition parallèle des mains gauches et mains droites sur les deux premières mesures peut alors être modélisée par le schéma suivant.
156Dans ce schéma, l’avancement du temps est visualisé par l’axe de gauche à droite, le positionnement des feuilles le long de cette ligne valant positionnement temporel. Le motif musical résultant, quoique toujours arborescent en termes de structures de données, apparaît comme une superposition de deux arbres qu’il faudrait dessiner dans un espace de dimension deux ; une dimension temporelle : l’écoulement du temps, et une dimension spatiale : la polyphonie.
157D’un point de vue informatique, il n’est pas nécessaire d’expliciter ce « collage » temporel des deux arbres. Chaque structure arborescente induit, par calcul, son propre avancement du temps. L’avancement parallèle dans les deux structures ne nécessite donc que la connaissance d’un seul point de synchronisation, par exemple le début des fenêtres de synchronisation. Ainsi, le positionnement temporel complètement explicité ci-dessus reste donc implicite dans la structure de donnée sous-jacente.
6. Expansion et contraction rythmique
158Dans les parties précédentes, nous avons défini un langage de composition de motif rythmique qui permet d’engendrer, à l’aide de compositions séquentielles et parallèles, les structures poly-rythmiques communément rencontrées en musique.
159Ceci fait, nous restons dans une description a posteriori de ces structures musicales. D’où peuvent provenir ces départs en anacruse ? Quelles peuvent être les intentions des musiciens et des compositeurs qui les utilisent ? Toussaint (Toussaint, 2010) propose une caractérisation mathématique de certaines structures rythmiques répétitives. Plus précisément, il démontre que la clave 3-2 fait partie d’un ensemble de répartition bien équilibrée de cinq battements sur seize. Mais comment produire a priori le balancement induit une telle structure rythmique ? Peut-on l’obtenir par transformation d’un battement régulier ? Le modèle proposé de profil temporel, enrichi d’un opérateur de resynchronisation non uniforme, appelé distortion, permet cela.
6. 1. Distorsion
160L’opération de resynchronisation modifie le profil temporel d’un motif rythmique sans changer la durée de sa réalisation. L’opérateur de distorsion présenté ici, au contraire, permet de modifier le profil temporel d’un motif sans changer la durée de sa fenêtre de synchronisation.
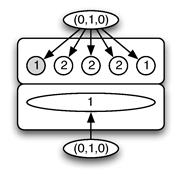
161Plus précisément, étant donné un motif m de profil W(m)=(p1,p2,p3), avec p=p1+p2+p3, on définit la distortion m[[a,b]] de m de facteur gauche a et droit b comme étant le motif obtenu à partir de m en prenant comme nouveau profil temporel W(m[[a,b]])=(p1–a.p,p2,p3+b.p).
162Cette distorsion peut être illustrée par le schéma suivant :
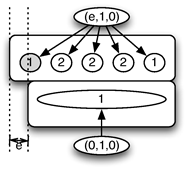
163L’exemple dessiné ci-dessus suppose que a≥0 et b≤0. En effet, en cohérence avec la définition de la resynchronisation, un facteur a (resp. b) positif se traduit a priori par un déplacement (relativement au motif joué) du point de synchronisation d’entrée (resp. de sortie) vers la droite. Au contraire, un facteur a (resp. b) négatif se traduit a priori par un déplacement du point de synchronisation d’entrée (resp. de sortie) vers la gauche. Bien sûr, en général toute généralité, le mélange de facteur droit et de facteur gauche positif ou négatif ne s’interprète pas aussi simplement.
164Dans tous les cas, la durée de réalisation du motif devant rester positif ou nul, on a, de façon analogue à la resynchronisation, la contrainte p1–a.p+p2+p3+b.p>0 c’est-à-dire a−b≤1.
165Remarquons que l’opérateur de distorsion est bien un opérateur dérivé de la resynchronisation suivie d’une repondération. On a en effet m[[a,b]] =(1+b−a).m[a’,b’] avec
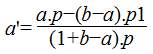
166et
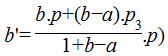
167En particulier, lorsque a =b, on vérifie que l’on a bien m[a,b] =m[[a,b]]. De plus, cette formule nous permet de lever, si besoin, toute ambigüité sur la sémantique de l’opération de distorsion : la resynchronisation ne change pas la réalisation d’un motif, la repondération l’étire ou le contracte uniformément.
168À la différence de la resynchronisation, l’opération de distorsion, qui inclue une repondération, modifie donc la durée des notes jouées dans les motifs rythmiques. Ces derniers sont en effet étirés ou contractés. Lorsque a≥0 (resp. b≤0) on parlera de contraction à gauche (resp. à droite) et lorsque a≤0 (resp. b≥0) on parlera d’expansion à gauche (resp. à droite).
169Pour finir la présentation de cet opérateur, remarquons que, pour la resynchronisation comme pour la distorsion, les facteurs a et b agissent relativement à durée de la réalisation du motif. Ce choix de modélisation fait que les opérateurs de resynchronisation et de distorsion permutent avec l’opérateur de repondération, i. e. pour tout a, b et k on a (k.m)[a,b] =k.(m[a,b]) (et donc (k.m)[[a,b]] =k.(m[[a,b]])). Cette propriété augmente le caractère compositionnel (au sens informatique) de ces opérateurs.
6. 2. Exemples de distorsion rythmique
170L’opérateur de distorsion peut être utilisé en représentation musicale afin d’engendrer quelques rythmes élémentaires à partir de rythmes plus élémentaires. Pour illustrer cela, nous analysons quelques lignes de basse qui se prête particulièrement bien à une analyse rythmique.
171Dans la musique populaire, la basse a en effet un double rôle, rythmique et harmonique. Ainsi, tout en donnant quelques indications sur la ligne rythmique générale du morceau joué, la ligne de basse, par sa fonction harmonique qui consiste surtout à jouer les accords, indique aussi comment structurer cette ligne rythmique support en cellules rythmiques consécutives correspondant à la réalisation de chaque accord. C’est l’analyse harmonique de la ligne de basse qui permet de faire apparaître anticipation et/ou prolongation rythmique.
172Regardons par exemple les trois lignes de basse ci-dessous.
173Sur une même structure harmonique – une même succession d’accords –, la première ligne est un exemple classique de basse binaire, la seconde décrit un accompagnement simple de Bossa Nova, et la troisième une ligne typique de Salsa.
174La cellule rythmique de la basse binaire associée à chaque accord est évidente. La fondamentale puis la quinte de chaque accord sont jouées sur le premier et le troisième temps de chaque mesure. On obtient donc le schéma rythmique suivant :
175Dans ce schéma, nous avons regroupé chaque note jouée avec le silence qui suit pour rendre compte des appuis. Les temps 1 et 3 sont des temps forts qui pourraient par exemple correspondre à un déplacement de pied droit sur une danse associée, le pied gauche bougeant en écho sur le silence qui suit.
176La cellule rythmique de la Bossa semble analogue à ceci près que chaque noire jouée est anticipée par une croche. Elle peut donc être représentée de la façon suivante :
177Nous pourrions bien entendu discuter de ce regroupement de chaque croche jouée comme anacrouse de la noire qu’elle précède. Cela pourrait correspondre à une règle générale de ligne de basse de musique populaire : chaque temps fort joué peut être précédé d’un appel, plus court. Du point de vue de l’analyse harmonique, ces croches permettent aussi, au changement de mesure et d’accord, d’anticiper la couleur harmonique de l’accord suivant. En effet, sur les accords de G7, Cmaj et Dm7, elles correspondent à la septième de l’accord qui vient.
178La cellule rythmique de la Salsa, connue aussi sous le nom de Tumbao, présente quant à elle une structure en anacrouse encore plus marquée et évidente d’un point de vue harmonique.
179La fondamentale de chaque accord est anticipée d’un temps. On peut ainsi décrire cette structure rythmique par le schéma suivant :
180Intentionnellement, nous représentons ici une succession de deux anacrouses pour rendre compte de l’aspect pulsé de cette musique, qui comporte toujours les mêmes temps forts sur le premier et le troisième temps.
181Que constate-t-on ? De la ligne binaire à la ligne de Salsa, les cellules et sous-cellules semblent être étirées pour créer une anticipation. Dans le cas de la Bossa, cette anticipation est uniforme, chaque sous-cellule de deux temps étant également étirée, par anticipation, d’une croche. Dans le cas de la Salsa, l’anticipation semble porter sur la mesure toute entière, en se répercutant deux fois plus sur la première sous-cellule que sur la seconde. Il apparaît que ces cellules rythmiques, typiques de la Bossa et de la Salsa, peuvent être produites comme distorsion du battement binaire.
182En effet, contemplons un instant la cellule rythmique du Tumbao (à gauche) Ne pourrait-on pas produire ce motif à partir de la cellule rythmique binaire analogue (à droite) ?

183Remarquons que la première note du Tumbao est retardée de 1 temps par rapport à la première note de la cellule binaire alors que la deuxième note du Tumbao n’est retardée que de 1/2 temps.
184Pour produire le Tumbao à partir de la cellule binaire, il suffit d’appliquer une expansion vers la gauche à la cellule de 4 temps en anticipant le premier temps de 1 temps, le second de 3/4 de temps, le troisième de 1/2 temps et le quatrième de 1/4 de temps, la cellule obtenue se résolvant tout de même sur le premier temps de la cellule suivante. En reprenant les représentations cycliques de Toussaint, tout se passe comme si ce Tumbao vient en quelque sorte s’enrouler autour du cycle binaire pour, in fine, se synchroniser avec lui. Cette métaphore peut être illustrée par le schéma suivant :
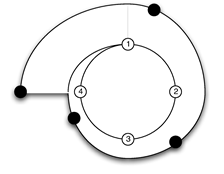
185Dans notre modèle, à partir du motif m codant le battement binaire, on fabrique simplement le Tumbao comme étant m[[−1/4,0]] soit une expansion à gauche de rapport 1 sur 4. Cette opération est illustrée par le schéma suivant :
186Remarquons par ailleurs que les facteurs de cette expansion sont indépendants de la durée du corps du motif initial. En pratique, cela signifie que l’opérateur de distorsion est indépendant de l’unité de temps choisie !
187Dans le même ordre d’idée, on peut aussi considérer une expansion à gauche de rapport 1 pour 3, c’est à dire m[[−1/3,0]] :
188Avec un silence comme première note, on obtient une structure ternaire :
189que l’on peut écrire :

190On peut aussi considérer une contraction de rapport 3 sur 4, soit le motif m[[3/4,0]], illustrée comme suit :
191On obtient ainsi ce qui ressemble à un appel pour le premier temps de la mesure suivante soit, schématiquement :
192ou encore

193Comme indiqué précédemment, pour modéliser ces structures avec introduction de durée négative, nous avons inséré un silence de durée relative de 12 croches.
194En faisant suivre l’appel ci-dessus construit par une simple cellule binaire, on construit les impulsions des deux premières mesures d’un morceau de pop célèbre : Another one bites the dust de Queen.
195Exercice : peut-on engendrer la totalité de cette structure rythmique à l’aide de composition séquentielle de distorsion de battement régulier ?
6. 3. Autres exemples d’interprétations rythmiques
196Dans la partie précédente, nous évoquons quelques exemples de contraction et d’expansion qui affectent la représentation musicale (classique) des structures rythmiques jouées. Nous montrons ici une autre utilisation de l’opérateur de distorsion propre à l’interprétation stylistique.
197Considérons par exemple ce motif de basse qu’on peut entendre, joué en ostinato, dans l’album Moonflower de Carlos Santana, exemple de musique latino-américaine :
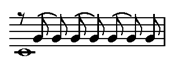
198Elle résulte, pour cet accord de Cmaj, de la composition parallèle de la fondamentale tenue – quasiment – sur toute la mesure, avec une série de quintes jouées sur les contre-temps.
199Ce motif peut être modélisé par la figure suivante :
200La vocation des contre-temps est ici de créer une sensation de roulement qui se résout sur le premier temps de la mesure suivante. Pour augmenter ce sentiment de roulement, le bassiste peut être tenté de « pousser » ces contre-temps, en les démarrant au début de la mesure avec anticipation pour, in fine, retomber sur le premier temps de la mesure suivante.
201Cette intention stylistique est modélisée dans la figure suivante :
202qui inclue une expansion des contre-temps de la forme m[[−e,1,0]], i. e. une expansion à gauche de facteur e sur 1.
203Autre exemple, une sorte de rubato de valse, qui relancerait l’appui sur le premier temps, peut être modélisée de façon analogue. En effet, on peut distordre chaque motif m joué sur une mesure de trois temps en m[[0,1,e]]. Cette expansion à droite pourra provoquer une impression de retard sur la pulsation régulière implicite. Cette sensation de retard se résout alors, presque soudainement, sur le premier temps de la mesure suivante. On amplifie ainsi l’effet tourbillon de la valse.
7. Conclusion
204Dans cet article, nous avons donc étudié quelques représentations possibles de structures ou motifs rythmiques classiques. Des opérateurs de combinaison simple : la composition séquentielle, les superpositions parallèles, les expansions et contractions, permettent de construire des motifs complexes à partir de motifs simples. Ces constructions sont illustrées à l’aide de nombreux exemples.
205Une notion de profil temporel, modélisé par des triplets de durées, qui n’est pas sans rapport avec les opérateurs PRE et POST de LOCO (Desain, Honing, 1988), permet de distinguer, pour tout motif rythmique, sa fenêtre de réalisation temporelle : quel est le motif rythmique, de sa fenêtre de synchronisation temporelle : quand doit-il être joué. En un sens, nous généralisons ainsi les marqueurs de synchronisation qui apparaissent dans les notations musicales classiques à travers la notion de barres de mesures.
206Fait nouveau cependant, la notion de profil temporel induit des opérateurs de resynchronisation et de distorsion applicables à tout motif rythmique. On obtient ainsi un modèle tout à la fois plus riche et plus souple que celui de Desain et Honing. En particulier, les opérateurs de distorsion permettent, par étirements et contractions non uniformes de structures rythmiques plus simples, d’engendrer de nombreuses rythmiques plus complexes.
207En matière de modélisation musicale, l’approche proposée ici doit maintenant être confrontée aux compositeurs, par exemple à travers une extension de logiciel de composition tel qu’OpenMusic (Bresson et al., 2009). Pour ce qui est du langage musical proprement dit, le modèle présenté ici pourrait sans doute être combiné avec l’approche (Fober et al., 2012). Les deux approches partagent un même but : la définition d’un langage combinatoire de composition musicale. La modélisation des anacrouses et prolongations proposées ici pourrait en effet permettre de donner un modèle formel aux opérateurs de haut-niveau proposés par ces auteurs. Enfin, rappelons qu’une implémentation de ce modèle, appliquée à la reconstruction audio ou au « control live-looping », est actuellement à l’étude (Berthaut et al., 2012).
Bibliographie
Agon, C., Assayag, G., Delerue, O., & Rueda, C. (1998), “Objects, Time and Constraints in OpenMusic.” In Proceedings of the International Computer Music Conference (ICMC), Ann Arbor, Michigan, October.
Allen, J., & Ferguson, G. (1997), “Actions and events in interval temporal logic.” In Oliviero Stock, editor, Spatial and Temporal Reasoning, pages 205-245. Springer Netherlands.
Assayag, G., Bloch, G., & Chemillier, M. (2006), “OMax-Ofon.” In Sound and Music Computing (SMC) 2006.
Assayag, G., & Bloch, G. (2007), “Navigating the oracle: a heuristic approach.” In ICMC’07. The In. Comp. Music Association.
Berthaut, F., Janin, D., & Martin, B. (2012), “Advanced synchronization of audio or symbolic musical patterns.” In Sixth IEEE International Conference on Semantic Computing.
Bresson, J., Agon, C., & Assayag, G. (2009), “Visual lisp/clos programming in openmusic.” Higher-Order and Symbolic Computation, 22(1), 3 2009.
Desain, P., & Honing, H. (1988), “Loco: a composition microworld in logo.” Computer Music Journal, 12(3):30–42.
Dubnov, S., Assayag, G., Lartillot, O., & Bejerano, G. (2003), “Using machine-learning methods for musical style modeling.” IEEE Computer, 10 :73-80.
Fober, D., Orlarey, Y., & Letz, S. (2012), « Composition de partitions musicales », Actes des Journées d’Informatique musicale (JIM 2012), p. 263-267.
Janin, D. (2012a), “On languages of one-dimensional overlapping tiles.” Technical Report RR-1457-12, LaBRI, université de Bordeaux.
Janin. D. (2012b), “Quasi-inverse monoids.” Technical Report RR-1459-12, LaBRI, université de Bordeaux.
Lawson, M. V. (1998), Inverse Semigroups: The theory of partial symmetries. World Scientific.
Lerdahl, F. & Jackendoff R. (1983), A generative theory of tonal music. MIT Press series on cognitive theory and mental representation. MIT Press.
Pachet, F. (2002), “The continuator: Musical interaction with style.” In ICMA, editor, Proceedings of ICMC, pages 211-218, Göteborg, Sweden, September, ICMA.
Toussaint, G. T. (2010), “Computational geometric aspects of rhythm, melody, and voice-leading.” Comput. Geom., pages 2-22.