L-Systèmes et formes musicales : quelles perspectives pour la musique générative ?

Jean-François Ducher

Résumé | Index | Plan | Texte | Bibliographie | Notes | Citation | Auteur | Version PDF | a | A

Résumés   

Index   

Index de mots-clés : composition, formes, L-systèmes, musique générative, fractales, CAO, algorithmes.

Plan   

1. Approches algorithmiques de la forme musicale

1György Ligeti définit la forme musicale, en adoptant un point de vue résolument analytique, comme la transformation « par une vue d’ensemble rétrospective, [du] déroulement temporel de la musique en espace » [1].

2La représentation spatiale d’une pièce s’opère dans différents plans correspondant à des critères d’analyse qui dépendent du style concerné (plan tonal, thématique, sériel, processus, etc.). Dans ces différents plans orientés par l’axe du temps sont positionnés des objets qui entretiennent des relations entre eux et avec l’ensemble. La forme ne peut être pensée indépendamment d’un historique qui a permis de structurer les capacités d’analyse de l’auditeur : une œuvre nouvelle s’inscrit dans (ou en rupture avec) des schémas formels préexistants.

3Du point de vue du compositeur, générer une forme musicale, c’est articuler des objets musicaux, établir entre eux des relations à différents niveaux de temporalité et leur donner une fonction dans l’ensemble. Ce faisant, les objectifs qu’il poursuit sont multiples et dépendent là encore du style. En général il s’agit de développer le matériau originel (thèmes, motifs, gestes, sons, textures, etc.) d’une façon intelligible pour l’auditeur, de lui donner un sentiment d’unité, de gérer sa mémoire en lui donnant des points de repère auditifs, de gérer son attention voire son implication dans le temps, par exemple, par la mise en œuvre d’un principe de variation, en alternant des phases de tension et de détente, ou bien encore en adhérant partiellement à un schéma formel prédéfini, pour mieux s’en distancier ensuite.

1.1. Dans les œuvres écrites

4Si on met de côté le champ d’expérimentation dans le domaine des formes ouvertes, le compositeur exprime le plus souvent une volonté de contrôle total de la forme de son œuvre qui exclut pour celle-ci le recours à des algorithmes de CAO.

5À titre d’illustration, considérons un environnement graphique de CAO largement répandu comme OpenMusic (OM). Open Music offre à l’utilisateur de nombreux modules algorithmiques de traitement ou de génération classés par librairies et représentés par des icônes. L’utilisateur peut graphiquement connecter ces modules entre eux et créer ainsi des programmes, appelés patchs, implémentant un objet musical complexe.

6Dès lors qu’il s’agit d’articuler les différents objets entre eux, pour travailler sur la forme d’une pièce, il existe dans OM une interface particulière appelée « Maquette » ; celle-ci combine l’idée du patch et celle du séquenceur : les traitements peuvent ainsi être disposés dans le temps de manière à former une partition virtuelle.

7La liberté du compositeur est totale, de même que son contrôle sur la forme, mais de façon symptomatique, l’assistance que propose l’environnement dans cette phase critique de la composition consiste à permettre un processus itératif, par tâtonnements en quelque sorte, de paramétrage et de juxtaposition des objets, puis de contrôle visuel et auditif du résultat.

8Indépendamment des outils informatiques de CAO, certains compositeurs se sont livrés ponctuellement à des expérimentations visant à utiliser des approches algorithmiques pour définir la forme de leurs œuvres.

9On citera par exemple dans le champ du sérialisme intégral l’exemple de Structures 1a (1952) de Pierre Boulez (voir l’analyse très complète de G. Ligeti au [2]) ou dans le cadre du « courant spectral » le cas de Tristan Murail qui utilise dans Serendib (1992), mais de façon très souple et limitée, des algorithmes fractals pour déterminer la structure temporelle de sa pièce [3, 4, 5].

10György Ligeti portait également un grand intérêt aux algorithmes fractals et à la théorie du chaos. Hebert Vázquez et Olivier Caravana montrent ainsi dans leurs travaux [6,7] sur sa première étude pour piano Désordre (1985) comment la polytemporalité voulue par le compositeur est mise en œuvre au travers de structures formelles auto-similaires à plusieurs niveaux.

11Un autre exemple remarquable est celui de Mikhail Malt [8] dans sa pièce Six Fractal Contemplations (2006), qui asservit l’intégralité de la forme de ses six pièces pour instruments et électronique à une courbe élémentaire à six points ; le matériau mélodique est généré par confrontation entre une courbe fractale idéale obtenue par auto-similarité à partir de la courbe « génératrice » et un matériau harmonique exogène.

1.2. Dans les œuvres génératives

12Nick Collins [9] fait le constat en 2009 que le sujet de la forme musicale dans les œuvres génératives, en particulier sous un angle psychologique prenant en compte l’expérience de l’auditeur, avait fait l’objet de peu de travaux académiques, à l’exception peut-être de ceux de Frederik Hedelin [10]. Hedelin est à l’origine d’un environnement orienté objet de CAO, Kimon, permettant de créer des modèles formels en concevant des objets musicaux de façon hiérarchique et en explicitant les interactions entre eux. Palle Dahlstedt1 fait remarquer à ce propos que si Kimon propose bien des outils de représentation structurelle de la forme, il n’assiste nullement le compositeur dans la génération de celle-ci en lui proposant des outils de nature à stimuler sa créativité.

13Dans la musique générative, la forme fait donc le plus souvent l’objet d’un arrangement sommaire, visant à articuler des moteurs générant le matériau sonore « microscopique » et tentant de concilier d’une part, la volonté de diversification de l’expérience de l’auditeur et d’autre part la reproductibilité de celle-ci ; on pense par exemple à la Lexikon-Sonate (1997) pour clavier de Karlheinz Essl [11], monument de la musique algorithmique, qui dispose de trois plans sonores distincts que viennent remplir de façon aléatoire 24 générateurs de structures.

14Ce relatif désintérêt pour les objectifs traditionnels des formes musicales peut s’expliquer en partie par le fait que, la plupart du temps, la dramaturgie des œuvres génératives provient moins de la musique en elle-même que de l’interactivité qui est recherchée entre l’installation musicale (ou le logiciel de musique générative) et l’auditeur ; ce dernier, mobilisé physiquement et intellectuellement, est invité à expérimenter lui-même l’impact du changement des paramètres en entrée des algorithmes – par l’interface utilisateur du logiciel ou par une interaction physique ou gestuelle avec l’installation. Dans les spectacles de live coding, l’interactivité est mise en œuvre, non plus avec l’auditeur, mais avec le compositeur-interprète.

15Une autre difficulté provient des caractéristiques intrinsèques des œuvres de musique générative : pour certaines, leur absence de début et de fin, du point de vue d’un auditeur qui va passer un temps indéterminé à les écouter ; ou bien encore, le fait que le compositeur ne peut établir qu’un modèle de forme, chaque instance de l’œuvre pouvant donner lieu à une forme en pratique différente.

16La question classique de la forme y est donc totalement renouvelée. Qu’il s’agisse d’œuvres écrites et plus encore, de musique générative, un champ de réflexion est donc aujourd’hui ouvert visant à trouver des algorithmes présentant des caractéristiques adaptées à la génération de formes musicales, c’est-à-dire remplissant les objectifs évoqués plus haut.

17Cet article va s’intéresser à une catégorie particulière d’algorithmes, les L-Systèmes, et s’attacher à évaluer leur utilité pour la communauté des compositeurs dans ce domaine.

2. Les L-systèmes

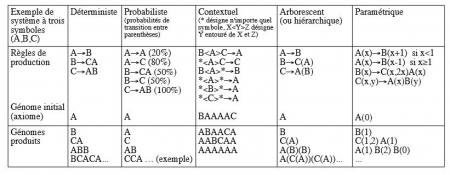
18Inventés par le biologiste Aristide Lindemayer en 1968, les L-systèmes sont historiquement un outil de modélisation du vivant par lequel on définit le devenir, de génération en génération, de certaines entités représentées par des symboles, sous forme de règles dites « de production » [12].

19Ces règles peuvent être déterministes ou probabilistes, dépendre ou non du contexte dans lequel se trouvent les symboles, placés dans un environnement linéaire – une chaîne de symboles – ou arborescent. Elles peuvent également dépendre des caractéristiques (ou paramètres) de ces entités.

Figure 1. Tableau de synthèse des différentes catégories de L-systèmes

Source : auteur

20Comme tout modèle, ce dernier doit ensuite donner lieu à une interprétation dans l’univers que l’on a cherché à modéliser : ce sont les règles d’interprétation du système.

21On ne peut, à propos des L-systèmes, dire qu’il s’agit d’un algorithme (vu comme une suite finie et non ambiguë d’opérations ou d’instructions permettant de résoudre un problème précis), puisque nous sommes plutôt en présence d’une façon « organique » de penser le monde. Il n’y a pas d’autre intelligence dans un système que celle qu’on amène à travers le modèle et son interprétation, d’une part, par les règles de production de l’autre. Toutes les catégories de L-systèmes évoquées ci-dessus (probabilistes, contextuels, arborescents, paramétriques) ont en commun cette logique de croissance organique du matériau, qui mathématiquement n’est rien d’autre que la mise en œuvre, de façon native, de la récursivité.

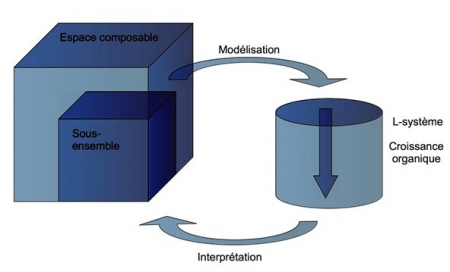
22La capacité de modélisation des L-systèmes a été étendue avec succès à de nombreux domaines scientifiques dont celui des fractales en mathématiques, en associant des opérateurs graphiques aux symboles du système.

Figure 2. Exemple d’interprétation graphique d’un L-système pour dessiner une courbe fractale (le flocon de Koch)

Source : auteur

23Les premières applications musicales des L-systèmes, dans le sillage des travaux de Prusinkiewicz et jusqu’au projet L-Muse, sont de simples transpositions des résultats obtenus par interprétation graphique sous forme de mélodies (éventuellement polyphoniques) données à jouer à des synthétiseurs MIDI. Une grande liberté est donnée au système pour déployer les différentes voix, les algorithmes utilisés ne prévoient pas de contraintes harmoniques ou contrapuntiques, sauf l’appartenance à une gamme ou un mode donné. La forme musicale, au sens où l’a pensée Ligeti, se confond littéralement avec son équivalent graphique. La musique, déconnectée de toute tradition stylistique, se fait naïve et illustrative.

24Le compositeur Hanspeter Kyburz, dans sa pièce Cellspour saxophone et ensemble (1994), se distancie de cette approche en affirmant ses impératifs stylistiques personnels et en donnant au L-système une responsabilité limitée sur la forme de certaines sections de sa pièce. Les symboles sont ainsi associés à certains objets musicaux polyphoniques identifiables à chaque occurrence par certaines de leurs propriétés (structure intervallique et rythmique, orchestration). Dans son analyse, Eres Holz [13] montre que la pièce est constituée de la juxtaposition des séquences résultant de l’interprétation des premières générations du génome produit ; en revanche, les modalités de variation des objets à chaque occurrence ne semblent pas être du ressort du L-système.

25Il cite Kyburz sur ses motivations à recourir à pareil procédé [14] :

L’algorithme est d’abord un classement de matériaux. Il aide simplement. Je regarde d’abord le matériau que j’ai esquissé et avec lequel j’aimerais travailler, et j’y aperçois surtout des conflits, des chances aussi, bien sûr, mais c’est encore très ambivalent. Je dois donc penser à la manière de construire ce matériau à partir d’une combinatoire, puisque je veux relier ces matériaux isolés entre eux.

26Les algorithmes servent ainsi à construire une continuité, puis à « générer un prototype » de la composition, qui permet à Kyburz d’acquérir un nouveau point de vue sur ce qu’il avait imaginé́ : « Parfois ils font exactement ce que je veux et parfois ils m’étonnent ».

3. Implémentation et retours d’expérience

27Une nouvelle implémentation des L-systèmes a été réalisée dans Max 7 ; elle s’appuie partiellement sur la librairie BACH pour la musique générative. Elle permet de gérer des L-systèmes probabilistes, (1,1) – contextuels, arborescents et paramétriques. Les règles de production sont rédigées en Javascript, ce qui permet de capitaliser sur la souplesse de ce langage pour manipuler les paramètres ; les génomes produits sont des lisp-like linked lists de BACH, des listes nativement arborescentes. Cette implémentation a été utilisée dans plusieurs champs d’expérimentation, du développement motivique jusqu’au pilotage de synthétiseurs granulaires, afin d’en tirer quelques enseignements.

28L’utilisation des L-systèmes pour modéliser certains univers composables et y proposer des formes se heurte d’emblée à un certain nombre de difficultés.

29Le cas de Cells montre que la logique organique (ou récursive) des L-systèmes peut-être adaptées à la mise en œuvre de certaines formes – en particulier, elle évoque intuitivement certains procédés de « développement continu ». Cependant, elle ne peut être universelle ni se plier à tous les besoins des compositeurs.

30Déterminer un sous-ensemble de l’univers composable pour lequel la modélisation sous forme de L-système présente un intérêt est donc une étape déterminante du processus compositionnel (figure 3).

Figure 3. Sous-ensemble de l’univers composable modélisé sous forme de L-système

Source : auteur

31Une fois les symboles du L-système associés sans ambiguïté à des objets dans l’espace composable (ou à des opérateurs agissant sur ces objets), apparaît une question délicate, qualifiée dans la littérature sur les L-systèmes de problème d’inférence : comment déterminer les règles de production adaptées à un objectif musical particulier ? Ce problème voit naturellement sa complexité augmenter avec le nombre de symboles dont il faut déterminer l’évolution.

32Face à lui, deux attitudes sont possibles : on pourra expérimenter et opérer par tâtonnements, ce qui est chronophage et ne garantit pas de résultat (sauf à renoncer complètement à un objectif musical prédéterminé) ; alternativement, on utilisera les L-systèmes pour résoudre des problématiques formelles simples, limitant au maximum le nombre de symboles du système.

33Les pionniers des applications musicales des L-systèmes avaient émis l’idée que ceux-ci, de par leur structure arborescente, pourraient naturellement gérer des polyphonies où les branches des génomes produits correspondraient à des voix (et la tentation était grande d’extrapoler en imaginant par exemple des polyphonies de processus).

34En réalité, deux symboles situés dans des branches différentes d’un génome ne sont pas dans le contexte l’un de l’autre (au sens des L-systèmes contextuels) donc il est difficile de prendre en compte, dans les règles de production, une contrainte qui porte sur leurs paramètres respectifs, ce qui exclut d’emblée, en particulier, une contrainte de nature harmonique ou contrapuntique.

35De telles contraintes doivent donc être gérées en aval de la production, sous la forme d’un processus de résolution de conflits à l’interprétation du génome ; on mettrait en œuvre une dialectique entre créativité (production) et normalisation (interprétation).

36Alternativement, il faut envisager de travailler dans un environnement peu contraint, par exemple, parce que les contraintes ont été déportées à l’intérieur des objets – eux-mêmes polyphoniques – ou bien encore, que les objets sont largement superposables (car appartenant à des plans sonores différents, ou pour d’autres raisons liées au style envisagé pour la pièce).

4. Exemple de mise en œuvre

37Un prototype2 utilisant les L-systèmes pour piloter, dans un cadre de musique générative, un sampleur rudimentaire3 construit dans MAX7 et BACH, va illustrer leur contribution sur un plan formel.

38Il s’agit de produire une polyphonie à 5 voix en glissement perpétuel dans un style qui peut évoquer celui de la musique de chambre pour orchestre à cordes de Giacinto Scelsi. Le sampleur est spatialisé sommairement à l’aide de la librairie d’ambisonie HOA.

39Le matériau de départ a été choisi pour son extrême simplicité, l’auditeur pouvant ainsi se livrer très simplement à l’analyse auditive du génome produit, identifier la valeur ajoutée du L-système et extrapoler les résultats avec d’autres matériaux plus complexes.

40Sur le plan harmonique, il s’agit d’une succession de 7 accords A₁ à A₇ obtenus par interpolation entre un accord harmoniquesur do₁ (A₁) et l’unisson sur do₄ (A₇). Le matériau est donc orienté, le resserrement des accords inharmoniques A₂ à A₆ amenant une certaine tension qui s’effondre ensuite sur A₇.

Figure 4. Matériau harmonique de base

Source : auteur

41De la même façon, on utilise exclusivement des samples correspondant à 7 modes de jeu d’un ensemble de cordes arco, M₁ à M₇. Les six premiers correspondent à des soli, avec une crispation progressive du jeu (compression des cordes, jeu tremolo sul ponticello, etc.), tandis que, dans un même souci de contraste, M₇ fait entendre l’ensemble au complet en position naturelle et legatissimo.

Figure 5. Samples : modes de jeu possibles

Source : auteur

42La forme générale voulue pour la pièce est un « X » si l’on pense au schéma des voix : on va globalement aller de A₁ à A₇ (processus P₁) puis retour sur A₁ (processus P₂) – mais dans la pratique les voix seront indépendantes. P₁ et P₂ ont également pour caractéristique de privilégier, pour le premier, les aigus et pour le second, les graves, l’accent est donc mis sur la jambe « descendante » du « X ».

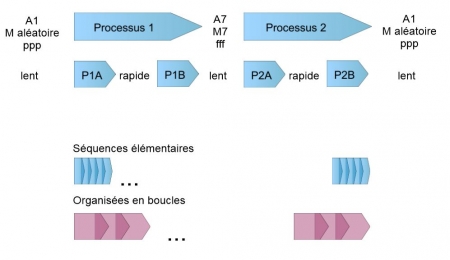
43Si les modes de jeu peuvent être aléatoires en début et en fin de pièce, les modes de jeu dont l’index est élevé se font de plus en présents à mesure qu’on se rapproche du centre, et l’arrivée sur l’unisson, point culminant de la pièce, se fait tutti (M₇). Les processus sont divisés en sous-processus en fonction du tempo sous-jacent (chaque processus donne lieu à une accélération puis une décélération), puis en séquences qui sont elles-mêmes organisées sous forme de boucles.

Figure 6. Décomposition de la pièce en processus et en séquences

Source : auteur

44Une séquence S est définie comme étant la transition d’un certain nombre de voix d’un pitch à un autre dans la combinatoire offerte par les accords A1 à A7, exécutée à un tempo donné, dans un mode de jeu donné, à une intensité moyenne donnée, et de façon tuilée avec les séquences précédente et suivante.

45Plus précisément, si on appelle N(i,j) la i-ème note de A_j, du grave à l’aigü, on définit S(a₁,a₂,a₃,a₄,a₅) comme une séquence où la voix i (si a_i>0) glisse de N(i,a_i) à N(i,a_{i +1}), si elle se situe avant le climax et de N(i,a_i) à N(i,a_i-1), si elle se situe après, sachant par ailleurs que si a_i= 0, par convention, cette voix i se tait.

Figure 7. Exemple de séquence S (1,1,6,3,3) dans P₁

Source : auteur

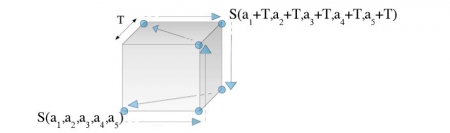
46Une boucle de taille T est un chemin aléatoire dans l’espace des séquences, choisi le long d’un cube à 5 dimensions de côté T et reliant un sommet donné au sommet opposé du cube.

Figure 8. Boucle (ici représentée en trois dimensions)

Source : auteur

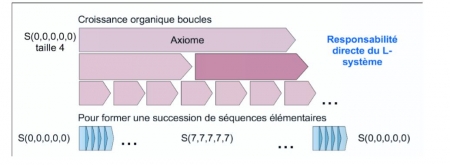
47Boucles et séquences sont les seuls objets connus du L-système ; la responsabilité de celui-ci est d’assurer la croissance organique des boucles : à partir d’une boucle de taille 4 partant du silence aux cinq voix, on obtient à chaque génération des boucles de taille toujours plus petite, jusqu’à ce que soit formée une succession de séquences S(a₁,a₂,a₃,a₄,a₅) partant du silence pour parvenir à A7 = S(7,7,7,7,7) et retourner au silence.

48Les règles de production, probabilistes, sont conçues de façon à maîtriser l’espérance statistique du rapport de proportions entre P₁ et P₂.

Figure 9 (a). Les productions du L-système

Source : auteur

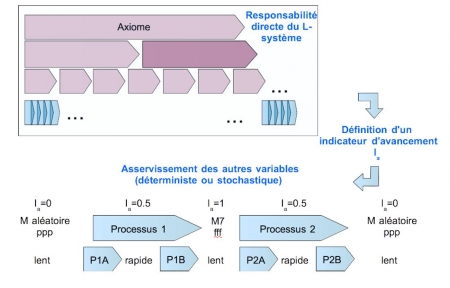
49Renversant la perspective formelle initiale, on va construire les processus autour d’un indicateur d’avancement compris entre 0 et 1, I_{a =} Σ_1≤i≤5 (a_i)/35. Dans P₁, I_a croît par une succession de vagues de 01 au point culminant de la pièce, puis dans P₂, il décroît jusqu’0.

50On va ensuite asservir de façon déterministe le tempo et l’intensité moyenne des séquences à Ia ; de la même façon, le mode de jeu sera un tirage aléatoire dans un sous-ensemble de {M₁, .. M₇} déterminé par la valeur de I_a (asservissement stochastique), de sorte que pour Ia = 0, le mode de jeu est totalement aléatoire tandis que pour Ia = 1, il est totalement déterministe et vaut M₇.

Figure 9 (b). Les productions du L-système

Source : auteur

51Il est également possible de définir des indicateurs d’avancement propres à une boucle et non-globaux, ce qui permet d’envisager de mettre en place des processus autour de points culminants secondaires, atteints dans une boucle, et non seulement autour du point culminant global de la pièce, comme ici.

52Dans ce prototype, toutes les autres variables (l’intensité d’une voix particulière, les paramètres de spatialisation) dépendent directement ou indirectement de la trajectoire dans l’espace des séquences : il n’y a donc pas de variables indépendantes du L-système, mais cela n’aurait pas posé de difficulté particulière d’y recourir.

5. Conclusion et pistes de réflexion

53Le prototype précédent illustre bien la valeur ajoutée que peuvent apporter les L-systèmes dans les processus de composition en musique générative. Peu normatifs, ils constituent une façon originale de penser la forme par croissance organique, compatible aussi bien avec l’approche traditionnelle du développement continu qu’avec une organisation par processus.

54Les travaux de recherche dans ce domaine pourront se poursuivre autour des axes suivants :

• identifier d’autres problématiques formelles pour lesquelles les L-systèmes peuvent apporter des réponses innovantes ; par exemple, on pourrait chercher à utiliser la capacité des L-systèmes contextuels à gérer la propagation, de génération en génération, de signaux dans le génome ;

• suivant en cela Manousakis [15], utiliser des L-systèmes en réseau afin d’aborder des problématiques (univers composables) plus complexes ; par exemple, si un L-système « maître » est en charge de l’agencement général des objets au niveau temporel le plus large de la composition, des systèmes « esclaves » peuvent avoir la responsabilité du processus de variation affectant les objets à chacune de leurs nouvelles occurrences ;

• approfondir la réflexion sur la prise en compte des contraintes compositionnelles au niveau de la production des L-systèmes, par le recours aux L-systèmes paramétriques ;

• identifier d’autres algorithmes ou techniques d’intelligence artificielle présentant un intérêt d’un point de vue formel, et pouvant s’articuler avec les L-systèmes - dans une logique de spécialisation de ces techniques.

55Sur le plan compositionnel, il est tout à fait envisageable, à condition de sophistiquer le matériau de base, de s’appuyer sur le prototype présenté plus haut pour réaliser une œuvre pour orchestre à cordes.

56Celle-ci pourrait être écrite en partant d’un des génomes produits, choisi selon des critères esthétiques subjectifs, ou mieux, réalisée dans l’esprit génératif avec une forme naturellement ouverte : chacun des musiciens recevrait les sections de sa partition (sur une tablette par exemple) au fur et à mesure du déroulé de l’œuvre, en temps réel, quelques secondes avant de devoir l’exécuter.

57Une telle œuvre poserait sans doute des challenges techniques et organisationnels passionnants, notamment pour le chef d’orchestre dont le rôle et le rapport aux musiciens pendant les répétitions et l’exécution doit être repensé. On pourrait enfin se livrer à une expérience « intermédiale » en associant le public à la boucle de « commande », c’est-à-dire en lui permettant de visualiser la partition qui se crée au fil du temps, soit au niveau des musiciens individuels, soit au niveau du conducteur global.

Bibliographie   

Notes   

Citation   

Auteur   

Jean-François Ducher