Préalables à une réflexion sur le temps musical et ses liens avec la physique contemporaine
Martin LalibertéDOI : https://dx.doi.org/10.56698/filigrane.342
Résumés
Résumé
Le vieux truïsme de la musique comme « art du temps » nous impose une importante remise en cause de nos certitudes, après plus de cent ans de découvertes fondamentales en physique relativiste, quantique, supersymétrique, cordiste ou branaire. Les sensibilités contemporaines musicales ont profondément évolué, cela est une certitude, mais quels liens pouvons-nous établir avec les spectaculaires mutations des connaissances physiques, en particulier les plus récentes ?
Cet article est le premier d’une courte série sur cette question, la matière abordée étant tellement abondante. Cette première étape passe d’abord en revue les connaissances classiques sur la question du temps, base de nos intuitions temporelles quotidiennes, puis effectue un premier résumé de l’évolution de la notion de temps en physique contemporaine. Un ou deux autres articles suivons pour sonder plus en détail les conséquences de cette mutation fondamentale des connaissances et en tirer des conclusions musicales.
Abstract
The old truism of music as an “art of time” requires a fundamental questioning of our certainties after over a hundred years of fundamental discoveries in relativistic, quantum, supersymmetrical, cord and brane physics. Contemporary musical tastes have undoubtedly shifted profoundly and significantly, yet what are the connections that may be drawn between the spectacular mutations of physical knowledge, particularly the most recent developments?
This article is the first in a short series devoted to this issue, since the material under study is particularly abundant. This first stage begins by reviewing some classical views of the question of time, the basis of our daily temporal intuitions, before providing an initial summary of the development of the notion of time in contemporary physics. One or two other articles will follow with a view to providing a more detailed examination of the consequences of this fundamental shift of knowledge and to establish some of the conclusions and implications of this shift in the specific realm of music.
Texte intégral
Introduction
1Le vieux truisme de la musique comme « art du temps » impose une importante remise en cause de nos certitudes, après plus de cent ans de découvertes fondamentales en physique relativiste, quantique, ou supersymétrique, et l’émergence des théories « cordiste » ou « branaire ». Les sensibilités contemporaines musicales ont profondément évolué, mais quels liens pouvons-nous établir avec les spectaculaires mutations des connaissances physiques, en particulier les plus récentes ?
2Cet article est le premier d’une courte série sur cette question, la matière abordée étant tellement abondante. Cette première étape passe d’abord en revue les connaissances classiques sur la question du temps, base de nos intuitions temporelles quotidiennes, puis effectue un résumé de l’évolution de la notion de temps en physique relativiste et quantique1.
Préalables
3Une étude des mutations de la notion de temps impose un rappel des nombreux préalables, savoirs implicites colorant la conception et la perception de chacun.
4Nous savons que la vie quotidienne rencontre partout des cycles (exemple 1).
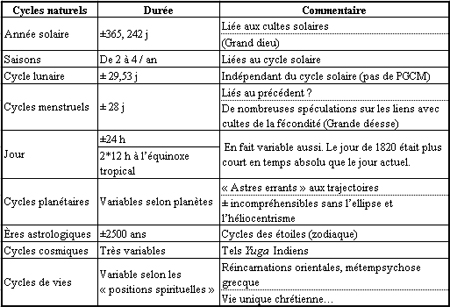
Exemple 1. De nombreux cycles.
5Ces nombreux cycles sont interprétés assez différemment selon les lieux, coutumes, croyances, comme le montre l’article « calendrier » de Wikipedia2. Deux positions philosophiques antiques se détachent pourtant.
Parménide et Héraclite
6Parménide et ses héritiers nient le passage du temps ou la réalité du mouvement. Ainsi, Zénon construit une série de paradoxes tentant de le démontrer : comment Achille pourrait-il rattraper la tortue puisque l’on peut toujours diviser leur écart un peu plus ?3
7Au contraire, Héraclite affirme l’impermanence de toute chose : « On ne se baigne jamais deux fois dans le même fleuve » : le changement permanent est la seule constante.
8Deux « temps » s’opposent donc, à l’aube de la civilisation occidentale : le temps bouclé, immuable et le temps linéaire orienté (exemple 2).
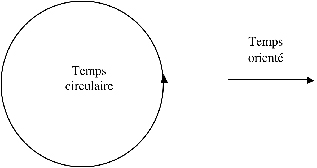
Exemple 2. Deux formes de temps élémentaires.
9L’opposition fondamentale de ces deux formes hante toute la tradition occidentale. Le cercle correspond au temps immobile, à la roue du temps, à l’éternel retour des cycles cosmiques ou terrestres4. La flèche est celle du devenir, du dynamique et de l’impermanent. Nous en retrouverons des échos partout dans cet article.
Conceptions chrétiennes
10Sur ces grandes positions fondamentales, se greffe la vision eschatologique chrétienne. La synthèse thomiste ressemble à peu près à ceci : des quasi-cercles concentriques mais combinés au temps orienté biblique (exemple 3).
11Cette forme est une synthèse intéressante du cercle de temps fermé et du temps orienté. Peut-être trouve-t-elle un écho dans les ellipses de Klee, croisement du cercle et de la flèche5 ?
12Si la place le permettait, une discussion de l’histoire des calendriers ou des appareils de mesure du temps serait utile à ce point. Le lecteur intéressé peut débuter ses recherches par les articles Wikipedia cités6. De même une discussion des moyens traditionnels de mesurer le temps, du gnomon primitif à l’horloge atomique serait utile.
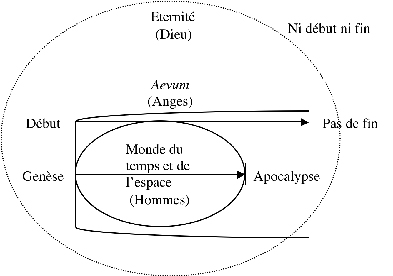
Exemple 3. Temps chrétiens.
13Il faut plutôt s’attarder un peu sur la conception baroque et classique du temps.
Les temps modernes (1600-1800)
14Les expérimentateurs de l’époque moderne — faisant suite à certaines idées d’Occam ou Bacon — entreprennent de vérifier les connaissances sur la nature du monde. Ils remettent en cause le sens commun élaboré depuis Aristote.
15Galileo Galilei, fils d’un musicien et théoricien fondamental de la musique baroque, entreprend autour de 1604 de vérifier les lois du mouvement aristotélicien. Il reprend le flambeau des grands théoriciens et expérimentateurs qui l’ont précédé, principalement Tycho Brahe et Johannes Kepler.
16Les travaux exemplaires de Galilée sur la chute des corps remettent tout en question et découvrent littéralement un « nouveau temps » :
« … un temps absolu universel, partout le même, qui s’écoule identiquement en tout point de l’Univers. Ce temps-là, indépendant de l’espace, autonome, par rapport aux phénomènes physiques, indifférent au mouvement, c’est ce qu’on appelle le temps newtonien. Il a l’avantage de donner au mot “maintenant” un sens parfaitement clair et distinct : ce qui se passe “maintenant” pour moi se passe également “maintenant” pour tous les autres observateurs dans l’Univers »7.
17Pour Galilée : « le livre de la nature est écrit en langue mathématique ».
18Sa conception du temps, vue du XXIe siècle se révèle toutefois assez contemporaine. Plutôt qu’un fil continu, il décrit le temps comme une suite « d’instants » mesurables (exemple 4).

Exemple 4. Le temps est une succession infinie d’instants
19Cette vision discrète du temps est étonnamment proche du temps usuel de l’ère informatique.
20Beaucoup serait encore à dire sur cette question. Le livre de Klein déjà cité effectue de nombreux rappels intéressants, en particulier grâce aux liens qu’il établit avec les théories physiques contemporaines.
Synthèses classiques
21Amplifiant et consolidant la mutation galiléenne, l’époque classique est celle de l’affirmation d’une causalité stricte et inévitable. Pour citer Leibniz : « rien ne se fait sans raison suffisante, c’est-à-dire que rien n’arrive sans qu’il soit possible à celui qui connaîtrait assez les choses de rendre une raison qui suffise pour déterminer pourquoi il en est ainsi, et non pas autrement »8. C’est le moment d’affirmation de la nature logique et vérifiable des lois de la nature.
22À la suite de Galilée, les scientifiques du XVIIIe siècle ont une conception assez claire du temps et de l’espace : il s’agit pour eux d’un cadre fixe, une sorte de contenant ou de scène, dans lequel les lois de l’univers interagissent (exemple 5).
23Ce cadre de référence est continu9, lisse, infini et éternel ; chacune de ces caractéristiques a une incidence concrète sur la physique et ses calculs.
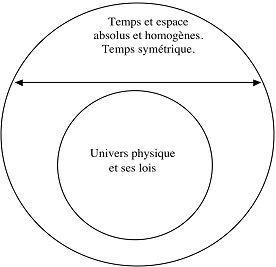
Exemple 5. Conception classique du temps et de l’espace.
24Il faut toutefois remarquer que la flèche du temps implicite est double. En effet, rien dans les équations de la physique classique ne permet de distinguer un sens privilégié du temps. Il peut circuler vers l’avant (temps ordinaire) ou vers l’arrière (temps inversé) sans « faire broncher » la plupart des équations10.
Newton (1687)
25Isaac Newton synthétise les travaux des générations antérieures et formule les lois fondamentales de la mécanique, de l’astronomie et de l’optique (exemple 6).
26Dans ces différentes équations, le temps devient vraiment une variable algébrique : « l’instant t ».
27Cette variable est exactement contemporaine des améliorations spectaculaires des instruments de mesure du temps : horloges à ressorts, chronomètres portatifs, etc.
28De nombreuses découvertes et inventions découlent de ces lois :
-
Principe de l’attraction universelle (gravitation et chute des corps),
-
Calcul intégral et différentiel (simultanément avec Leibniz),
-
Calcul vectoriel (les forces agissent dans des espaces, nature géométrique des forces),
-
Travaux sur la lumière et les ondes (avec Huygens),
-
Relativité classique (de Galilée),
-
Loi de la conservation de l’énergie,
-
Autres applications de l’idée d’attraction (magnétisme, chimie, voire en littérature11)…

Exemple 6. Principes de Newton et autres définitions fondamentales.
29Jusqu’à un certain point, à l’échelle humaine12, nous avons peu dépassé ce niveau ; la physique de Newton est celle de notre quotidien.
Paradoxes et insuffisances
30Pourtant, au moment même du triomphe de la physique classique, des problèmes demeurent13 :
31Comment se transmet la force gravitationnelle ? Sa vitesse (et celle de la lumière) est-elle vraiment instantanée ? Quel est son médium, son support, son vecteur ?
32Les lois de la physique se révèlent être les mêmes pour tous les systèmes : la relativité de Galilée explique, par exemple, que l’on peut jouer au ping-pong dans un train en marche. Que devient alors le temps linéaire postulé et utilisé ?
33On a remarqué que le « sens » du temps ne joue aucun rôle : la physique newtonienne demeure essentiellement identique si on se dirige vers le futur ou vers le passé14. Quelle est alors la nature du temps si toutes les équations temporelles sont réversibles ? Un temps réversible au niveau des lois physiques implique-t-il réellement une possibilité de retour dans le temps, voire un bouclage du temps sur lui-même ? Ces interrogations amènent un certain retour à la position de Parménide ou Zénon : négation du temps, du mouvement réel ou de l’espace. Enfin, les outils mathématiques fonctionnent à l’intérieur de limites : si l’on peut étudier avec précision les attractions réciproques de deux corps, le « problème à trois corps » est insoluble en toute rigueur15. Alors, comment décrire l’infini de l’univers, avec ses innombrables interactions ? Faut-il être un démon pour y arriver ?
Le temps au XIXe siècle
34Avec l’électromagnétisme16, la thermodynamique, science de la chaleur, de l’énergie et des systèmes est une des principales réussites scientifiques de l’époque de la révolution industrielle.
Principes de la thermodynamique
35Ce domaine fait ses premiers pas17 dès 1811-1822 (Joseph Fourier) et connait des formulations de plus en plus élaborées et strictes au cours du XIXe siècle (Sadi Carnot, Clausius, Hamilton…), jusqu’à la version définitive de Boltzmann de 1872. Quatre grands principes sont établis :
-
Principe 0 : si deux systèmes sont équilibrés avec un troisième, alors il y a équilibre entre eux. Ce principe permet de définir la température ;
-
Principe 1 : la variation totale d’énergie (U) d’un système se fait par échange de travail (W) et de chaleur (Q) : ∆U = ∆W + ∆Q18. Loi stricte de la conservation de l’énergie ;
-
Principe 2 : l’entropie S d’un système ne peut que croître (ou rester constante). À l’équilibre, S tend vers S max.
-
Principe 3 : au 0 absolu (-273, 16 °C), un corps n’a plus aucune énergie d’excitation ; l’entropie est alors nulle.
36Le second principe est absolument impitoyable : dans toute situation, le désordre d’un système fermé ne peut que rester constant ou croître. Les hautes énergies s’affaiblissent, le froid et le chaud deviennent tièdes, l’ordre tend à se détruire19. S’il est facilement admis par le sens commun (« tout se dégrade »), ce principe réfute la réversibilité temporelle de la physique classique. En effet, ce second principe fonde de façon stricte la possibilité d’un temps réel, orienté, d’un devenir possible :
37La « flèche du temps » thermodynamique, pour reprendre le terme d’Arthur Eddington en 192920, pourrait donc se définir ainsi (exemple 7).

Exemple 7. Flèche du temps entropique.
38Les tentations du cercle temporel se transforment en vision de spirales évolutives21.
39Toutes les expériences, les plus fines et précises, s’accordent avec les études mathématiques : l’entropie croît inexorablement. Visions de la mort froide du monde…
40Cela dit, les équations de l’entropie sont implicitement symétriques : le désordre est plus probable que l’ordre, tant dans le passé que dans le futur22. C’est l’ordre qui est improbable, partout et toujours. Dans ce cas, il est très étonnant que notre univers ait pu avoir à ses origines une phase hautement ordonnée. La physique relativiste propose une explication de cela23. Ces réflexions thermodynamiques provoquent beaucoup de nouvelles interrogations.
Questions, contradictions et démons
41Comment concilier la réversibilité temporelle de la physique classique et le second principe ? Que devient le déterminisme, la causalité pure ? Rapidement, les chercheurs pressentent des limites. Avant la thermodynamique Laplace espère un démon capable, en sachant toutes les positions des molécules d’un gaz et leur vitesse, d’en calculer (prédire) l’avenir exact tandis que Maxwell rêve d’un autre démon capable d’inverser toutes les directions et les vitesses, ramenant ainsi un système à son point de départ. Cela démontrerait la réversibilité classique.
42On le voit, cela dépasse les capacités humaines.
Statistiques de Boltzmann
43En 1872, Ludwig Boltzmann, personnage quelque peu tragique d’une phase de transition de la physique24, tente de formaliser les calculs thermodynamiques de façon plus complète pour répondre à ces interrogations. Ne pouvant calculer de manière exhaustive toutes les trajectoires des molécules d’un gaz, il doit se résoudre, un peu malgré lui, à imposer une analyse statistique des gaz et découvre ainsi un lien fort avec l’entropie : S = k ln Ω25.
44Ses équations imposent d’abandonner tout espoir déterministe pour les éléments individuels : dans des systèmes macroscopiques réels, la quantité d’événements est telle que seules les statistiques et les lois des grands nombres permettent d’y voir clair. L’entropie serait alors une « propriété émergente » des systèmes macroscopiques. L’orientation du temps que l’on peut observer au quotidien ne se déduit pas des phénomènes microscopiques individuels mais de leur action commune. Le déterminisme et la causalité stricts (les trajectoires individuelles) sont donc remis en cause bien que ces principes soient réaffirmés avec une très grande clarté de façon statistique.
45Cette mutation statistique de la compréhension du monde est fondamentale pour la physique contemporaine, de Planck aux physiciens quantiques et au-delà. La crise scientifique vécue par Boltzmann, provoque une série de recherches nouvelles, en rupture avec les certitudes trop rapides du XIXe siècle.
Le temps relativiste
46La physique du XXe siècle connaît deux principaux domaines, liés aux échelles spatiales cosmiques et subatomiques. Premier domaine, la physique à grande échelle et des mouvements très rapides a des impacts très profonds sur la conception rigoureuse du temps et de l’espace.
Des problèmes vers 1900
47L’électromagnétisme de Maxwell est brutalement remis en cause par une expérience « de routine » : en 1887 à Cleveland, Michelson et Morley obtiennent en mesurant la vitesse de la lumière dans différentes directions des résultats incompatibles avec la théorie admise26. Selon la théorie de l’époque, la vitesse de la lumière aurait varié selon la direction du mouvement de l’observateur, par exemple en direction de la source lumineuse ou dans la direction opposée. Les mesures montrent qu’il n’en est rien.
48Pourquoi ces résultats inattendus ? Quelle est donc la vitesse de la lumière, dans ce cas ? Quelle est la véritable nature de la lumière ? Si elle est une onde, quel est son milieu de propagation ? L’éther postulé par Maxwell existe-t-il ?
Relativité restreinte (1905)
49Einstein résout ces problèmes en admettant les résultats expérimentaux et en ayant le courage de tout remettre en cause :
501. La vitesse de la lumière dans le vide est immuable : la constante c est la célérité de l’onde27 lumineuse dans le vide (±2,99 * 108 m/s). On ne peut ni la ralentir ni la dépasser ;
512. Il y a équivalence de l’énergie et de la masse28 : E = mc2 ;
52Si la vitesse de la lumière est absolue et l’énergie équivalente à la masse, toute accélération augmente la masse et tout changement de masse implique des changements d’énergie. Une particule matérielle ou une onde ne peut donc jamais dépasser la limite de c, elle ne fait que s’alourdir. Cette équivalence de la masse et de l’énergie est la source des hautes énergies atomiques et nucléaires : c étant très rapide, peu de masse donne beaucoup d’énergie.
533. Dans ces conditions, l’espace et le temps ne peuvent plus être fixes, mais deviennent relatifs à la vitesse des observateurs et des objets en mouvement. Ce qui est fixe désormais est « l’intervalle » spatio-temporel : s = c2(t2-t1)2-(x2-x1)2-(y2-y1)2-(z2-z1)2 29 (exemple 8).

Exemple 8. Contraction de l’espace dans l’axe d’un mouvement très rapide30.
54Développons un peu ce troisième point, crucial pour le temps.
55Tout d’abord, la nouvelle compréhension du monde d’Einstein entraîne de formidables conséquences : le temps et l’espace ne sont plus absolus, mais varient selon la vitesse des observateurs. Ils ne sont plus indépendants, non plus. Pour faire sens, les anciennes dimensions d’espace (trois dimensions x, y z) et le temps (t) se retrouvent inextricablement liés dans un tout nommé le continuum espace-temps31. Tous les calculs physiques doivent désormais se faire dans un « espace » mathématique à 4D32. Il y a conservation du mouvement mais en liant impérativement ces quatre dimensions.
56On retrouve alors différents cas de figure : un objet au repos concentre toute son énergie à se déplacer dans le temps. S’il se déplace dans l’espace, le déplacement temporel se retrouve affecté : donc, la vitesse modifie l’écoulement du temps. En pratique, il faut toutefois atteindre des fractions importantes de la vitesse de la lumière pour que ces phénomènes jouent de manière importante. Cela se produit dans les collisionneurs de particules, où des particules de durée de vie très brève « vivent » plus longtemps que prévu, à cause de leur ralentissement relativiste.
57D’autre part, et cela est fort troublant pour le sens commun, le temps acquiert ainsi une propriété quelque peu « spatiale » : il devient une dimension dans laquelle les choses évoluent, mais il ne s’écoule plus !33 La physique contemporaine prend ainsi un tournant géométrique frappant. Par exemple (exemple 9), voici trois personnages :
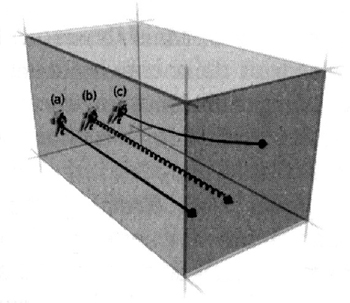
Exemple 9. Trois trajectoires dans l’espace-temps : a) immobile dans l’espace b) en rotation dans l’espace et c) en accélération34.
58Dans cette représentation simplifiée35 en forme « de miche », l’un des personnages est immobile et parcourt le temps (sens de la flèche) en droite ligne, le second tourne sur lui-même, ce qui crée une forme hélicoïdale dans l’espace-temps et le troisième accélère vers le haut. Les mouvements ont ainsi des formes spécifiques distinctes si on inclut le temps ou pas. Le cercle b) devient une hélice, le point de a) une droite et l’accélération verticale de c) une courbe.
59Dans l’exemple suivant, deux observateurs éloignés regardent la « miche d’espace-temps » avec des angles différents, ce qui provoque une perception différente du temps. À cause de l’angle36, la « date » d’un événement quelconque devient relative (exemple 10).

Exemple 10. Des « tranches » de temps relatives entraînent des divergences d’appréciations sur le moment exact d’un événement37.
60Lorsque l’on croise ce phénomène avec la vitesse limitée de la lumière, on obtient les célèbres cônes de lumière, les zones d’influence possibles d’un événement sur son futur, via des ondes électromagnétiques (exemple 11).
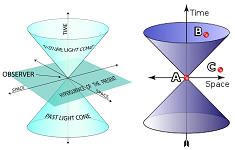
Exemple 11. Cônes de lumière autour d’un événement spatio-temporel38.
61Ici, B peut être influencé par A, mais pas C. La vitesse limitée de la lumière pose ainsi des limites absolues à la communication ou aux relations causales. De nombreuses opérations géométriques en découlent39. Depuis 1905, la topologie et la géométrie algébrique à 4 dimensions40 deviennent les outils courants des sciences physiques.
62L’opposition du cercle et de la flèche du temps prend alors une nouvelle forme (exemple 12) :
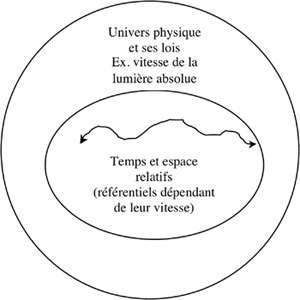
Exemple 12. Conception relativiste.
63L’ellipse centrale contient désormais l’espace-temps relatif aux mouvements et aux vitesses, dans le cadre général (cercle extérieur) des lois physiques absolues41. On constate donc un reversement de la hiérarchie classique : le temps fait partie du variable, pas de l’absolu. Remarquons aussi que cette ellipse centrale est réellement multidimensionnelle. Le troisième point d’intérêt est que la flèche du temps demeure réversible. Comme bon nombre d’écrivains de science-fiction s’en sont rendu compte dès H. G. Wells (1895)42, le voyage dans le temps ne semble pas exclu de cette description du monde.
64Pour découvrir la théorie de la relativité, Einstein avait cependant considérablement simplifié la situation en omettant deux aspects fondamentaux de la nature : le mouvement accéléré et la gravitation.
Relativité généralisée (1915)
65Pour remédier à ce problème, Einstein élabore ensuite une théorie relativiste de la gravitation universelle qui complète la relativité restreinte.
661. Comme précédemment, l’espace et le temps ne sont plus indépendants, mais forment un tout à 4D.
672. Il y a équivalence locale entre la masse inertielle et la masse gravitationnelle ; c’est-à-dire qu’un observateur ne peut distinguer le mouvement accéléré de l’attraction gravitationnelle avec ses seules observations locales. Ainsi, un aviateur en courbe de vol accentuée se sent parfaitement en apesanteur ou bien un cylindre en rotation (cela est du mouvement accéléré) rétablit une gravité artificielle dans une station spatiale .
683. La masse courbe l’espace-temps43 ; cela est la principale différence entre les deux versions de la relativité. Cela permet de redéfinir l’attraction gravitationnelle sur une base relativiste. Celle-ci peut s’exprimer ainsi (exemple 13).
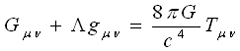
Exemple 13. Équation d’Einstein.
69Où G est la constante gravitationnelle de Newton, c la vitesse de la lumière, Tµ un « tenseur » mesure de la densité de matière et d’énergie, Gµla mesure de la courbure et gµ la constante cosmologique44. La courbure de l’espace-temps dépend directement de la quantité d’énergie/masse45 (exemple 14).

Exemple 14. Courbures de l’espace par un corps céleste, a) en deux dimensions, b) en trois dimensions46.
70On remarque aussi que la grosse sphère (le soleil) déforme beaucoup l’espace-temps tandis que la petite en a) (la terre) la déforme moins. La force gravitationnelle est donc une mesure de cette courbure de l’espace. L’espace de Minkowski, plat (pseudo-euclidien), se retrouve courbé (pour devenir pseudo-riemannien47). Dans l’espace ainsi courbé, il n’y a plus de droites mais des « géodésiques »48 (exemple 15).
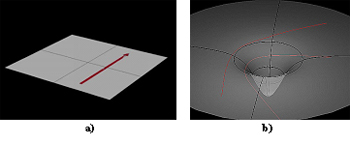
Exemple 15. a) Espace plat et droite et b) espace courbé et géodésiques49.
71Est-ce cela qui trouve un écho étonnant chez Tolkien ?
« Avallónë is vanished from the Earth and the Land of Aman is taken away, and in the world of this present darkness they cannot be found. Yet once they were, and therefore they still are, in true being and in the whole shape of the world as at first it was devised … All roads are now bent … Therefore the loremasters of Men said that a Straight Road must still be, for those that were permitted to find it. And they taught that, while the new world fell away, the old road and the path of the memory of the West still went on, as it were a mighty bridge invisible that passed through the air of breath and of flight (which were bent now as the world was bent) … »50.
72Les rêveurs imaginent tout de suite des hyperespaces, « facteurs de distorsion », « trous de vers » et autres chemins directs permettant d’aller plus vite que la lumière51.
73La courbure de l’espace calculée en 1915 par Einstein est confirmée dès 1919 par des mesures précises de la position apparente des étoiles lors d’une éclipse. Plus récemment, la courbure autour de la terre a été mesurée en bon accord avec la théorie (0,5 % d’écart)52. Pour reprendre une expression célèbre due à John Archibald Wheeler : « la masse et l’énergie disent à l’espace-temps comment se courber, et la courbure de l’espace-temps dit à la matière comment se comporter »53. Einstein et ses collègues disent aussi que le temps est le moyen pour que tout ne se produise pas en même temps54.
744. Similairement, les masses (et les hautes énergies) courbent le temps. Dans cette nouvelle compréhension des choses, plus on va vite, plus la masse augmente, plus l’espace se courbe et plus le temps ralentit ! Ainsi, les jumeaux de Langevin (ou deux horloges atomiques) se décalent dans le temps si l’un reste fixe et l’autre voyage vite. À la limite, à la vitesse de la lumière, le temps cesse d’avancer ! Pour un photon, aucun temps ne s’est écoulé depuis le Big Bang et il ne s’est pas déplacé (géodésiques d’espace et de temps nulles).
75Le temps se retrouve donc « propre » à un référentiel donné : le temps propre se distingue du temps ordinaire T ou t. Différents calculs de ce t sont possibles, en fonction des masses en présence et de leurs mouvements55. Par exemple, dans le cas d’une boîte accélérée s’éloignant de son point de départ, la dilatation temporelle peut être calculée ainsi (exemple 16).
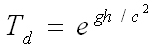
Exemple 16. Dilatation temporelle.
76où Td est la dilatation temporelle au point éloigné, g est l’accélération de la boîte par rapport au point de départ, h est la distance verticale entre les observateurs. Lorsque gh est nettement plus petit que c2, l’approximation linéaire suivant peut aussi être utilisée : Td = 1 + gh / c2.
77Ainsi, un ascenseur s’éloignant de sa base avec une accélération de 10 m/s2, à 100 m de la base voit son temps dilaté d’un facteur : 1,000000000000011265, soit quasiment rien car c2 est un nombre énorme56. Par contre un appareil très rapide57 accélérant à 200000000 m/s2, à 1000000 m de sa base connaît un facteur de dilatation de 1,02225. Des horloges atomiques sur des avions en mouvement ont prouvé ces résultats.
Expansion et destin de l’univers
78En résolvant attentivement les équations, on retrouve une conséquence de la relativité généralisée : l’univers est en expansion rapide. Cela semblait impossible au père de la relativité qui concevait plutôt un univers statique : éternel et immuable comme les lois de la géométrie. C’est la raison pour laquelle il a introduit la constante cosmologique dans ses équations, sorte de « freinage » de l’expansion58 implicite de la formule initiale59.
79Cependant comme l’ont assez rapidement démontré les astronomes comme Hubble (1929), les galaxies s’éloignent l’une de l’autre, à grande vitesse, tout en augmentant d’autant le volume de l’univers (les galaxies sont comme des raisins dans une pâte qui lève). On a donc retiré la constante cosmologique des équations et repris la formulation initiale d’Einstein. Nouveau renversement, depuis les années 1980, une théorie très convaincante (Guth, Englert, Starobinsky) sur le Big Bang remet en selle la constante cosmologique, dans une interprétation différente60.
80L’univers a donc débuté dans un tout petit volume et s’est dilaté, tout en se refroidissant. Le temps a donc un début : le Big Bang et une direction : de l’origine vers l’expansion. Ce serait la raison de toutes les causalités et de la flèche entropique. On progresse de l’ordre initial — « l’inflaton » de Guth explique pourquoi il y a dilatation61— vers l’état actuel de l’univers, dilaté, à basse température moyenne et faible densité de matière mais avec des îlots d’ordre local : galaxies, amas, systèmes de planètes (exemple 17).
81Les différents angles de courbure de cette forme sont à remarquer. Le début est en expansion très rapide : il explose à 1030 ou 1050 fois le volume initial en l’espace de 10-35 secondes ! On parle alors de la période « d’inflation ». Ensuite, la vitesse d’expansion réduit considérablement et se stabilise (courbe plus droite). Enfin nous assistons depuis 7 milliards d’années à une expansion accélérée de l’univers mesurable. On impute cela à la présence de matière et d’énergie indétectable (« noire »), rendant l’univers beaucoup plus massif et énergétique que prévu62.
82La similarité de cette forme avec celle de l’ex. 3 est frappante, peut-être n’est-elle pas accidentelle. La théorie du Big Bang — mais pas son nom63— a été formulée et défendue par Georges Lemaître (1927-31), physicien à l’université de Louvain et chanoine. L’interprétation créationniste de cette découverte ne lui a pas échappé, mais il faut ajouter qu’il faisait une lecture plus symbolique que littérale des Écritures64. Il a en fait contesté auprès du Pape l’intégration de la théorie du Big Bang dans le credo catholique par Pie XII65 et infléchi un peu ce dogme.
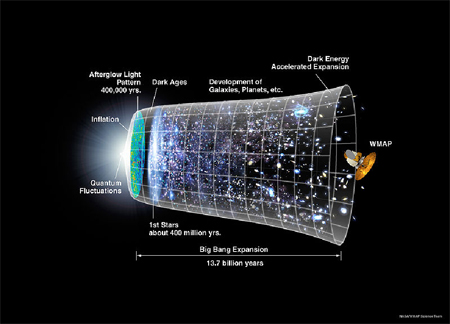
Exemple 17. Big Bang et expansion cosmique66.
83On peut tout de même se demander si des physiciens hindouistes auraient découvert la même « forme » de temps. La montée en puissance scientifique de l’Inde ou de la Chine pourra nous apporter des nouveautés formelles intéressantes.
84Le futur à long terme de l’univers est actuellement incertain67. Trois grandes théories s’affrontent : celle de la mort thermique (Big Freeze), celle du Big Crunch et celle du Big Bounce. La première — similaire à la mort froide du XIXe siècle —, semble actuellement la plus probable. L’univers continuera à se dilater jusqu’à sa dissolution et son extinction énergétique68. La seconde fait, après une extension maximale, rebrousser le mouvement de la matière vers l’origine jusqu’à une extrême concentration (implosion) finale. Il est à remarquer que dans ce cas la flèche du temps et de la causalité s’inverse mais que la plupart des phénomènes physiques demeure similaire, vue la symétrie des équations fondamentales69. La dernière — similaire à certaines intuitions hindouistes70 — alterne les explosions (Big Bang) et les implosions (Big Crunch) pour créer des « rebonds » cosmiques (Big Bounce). Plusieurs raisons et causes expliqueraient l’une ou l’autre de ces théories : excédent ou non de matière-énergie, théorie des cordes et des « branes », etc.
85Seule la première hypothèse entraîne une durée illimitée de l’univers, mais n’exclut pas un vidage de sa substance et de son énergie. Dans ce cas, la matière arriverait tôt ou tard à un terme, mais lentement71. Les deux autres hypothèses impliquent des « catastrophes » mettant un terme spectaculaire à l’univers tel que nous le connaissons. Enfin, il est assez clair que l’éternité ne fait pas partie des hypothèses scientifiques dominantes actuellement72
86Dès les années 1930, les résonances de ces découvertes ont interpellé les chercheurs et conforté certains occidentaux dans leur curiosité pour les ouvrages de philosophies et religions orientales : Oppenheimer73, Heisenberg, Schrödinger et bien d’autres Capra74.
87Indépendamment des croyances et des explications officielles ou intimes, jusqu’à ce jour toutes les expériences n’ont fait que confirmer la validité de théorie de la relativité généralisée, du moins à moyenne et grande échelle75. C’est une des théories scientifiques qui s’accorde le mieux avec l’expérimentation la plus fine de l’histoire occidentale : on obtient une précision de dizaines de décimales de 1 % dans certaines conditions. Il faut désormais des collisionneurs de particules à énergies extrêmes pour aller au-delà de cette précision. C’est tout l’enjeu du LHC du CERN, récemment inauguré.
88Il faut maintenant changer d’échelle car la compréhension actuelle du temps en est fondamentalement tributaire.
Le temps quantique (1900-1970)
89Il s’agit du second grand domaine de la physique contemporaine, à l’échelle inverse, atomique et subatomique, cette fois.
Quanta (1903)
90En effet, une autre théorie s’impose pour expliquer les détails des fonctionnements énergétiques et, surtout, la nature et la structure atomique : la théorie des quanta. À partir des travaux de Planck (1903) sur l’énergie des corps noirs, les physiciens admettent la nature discontinue à l’échelle microscopique des niveaux énergétiques : l’énergie procède par sauts quantifiés, sans transition (exemple 18).
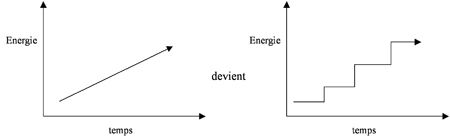
Exemple 18. Énergie classique continue et énergie quantique à paliers discrets.
91Ainsi, le photon d’Einstein est le quantum, l’unité élémentaire, de l’énergie lumineuse. Cela semble lui conférer une nature corpusculaire contredisant l’étude de la lumière en termes d’ondes, mais rejoint une longue histoire depuis le 1er millénaire76, pour ne parler que de notre civilisation.
Nature duale de la lumière (1905)
92Pour rendre compréhensible le comportement de la lumière, il faut en effet oublier l’ancien éther des physiciens du XIXe siècle et admettre que la lumière est à la fois une onde (théorie électromagnétique) et un corps (théorie corpusculaire)77. Il semble en effet que les grains de lumière, les photons, sont leur propre support ondulatoire. La masse des photons est nulle : ils peuvent donc atteindre la vitesse limite. Comme on l’a vu supra, le temps n’existe donc pas pour eux. Est-ce l’éternité ?
Atomes (1900-1940)
93Le point de vue quantique permet d’élaborer dans le détail une explication de la structure des atomes et des mécanismes physiques et chimiques (exemple 19).
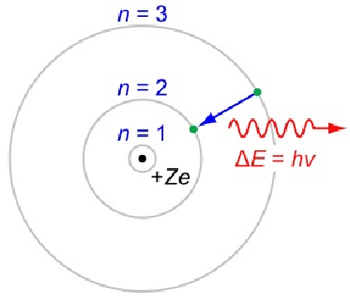
Exemple 19. Atome (modèle de Bohr simple).
94Ceci est le modèle orbital, ce « système solaire en miniature » qui fascine les amateurs de correspondances et qui est bien passé dans la culture commune. Le point vert est un électron, le point noir un noyau atomique et la courbe rouge un photon. La flèche bleue indique que l’électron quitte une orbite de plus haute énergie pour une orbite de moindre énergie et que la différence est émise sous la forme d’un photon doté d’une certaine fréquence . h est la constante de Planck. Ce modèle initial souffre toutefois de nombreuses difficultés. Tel quel, il est instable et ne peut expliquer complètement les données expérimentales.
Probabilités (1926)
95La réalité est donc plus complexe : après étude approfondie, il s’avère que toutes les données quantiques sont de nature essentiellement statistiques. Born (1926) démontre que la position des électrons s’effectue réellement en termes de probabilités de présence à un endroit donné, probabilités données par l’équation de Schrödinger (exemple 20).
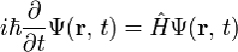
Exemple 20. Équation de Schrödinger.
96Où i est la part imaginaire, ħ est la constante de Planck divisée par 2π, est la fonction d’once (amplitude de probabilité) pour différentes configurations du système, Ĥ est l’opérateur hamiltonien, r est la position (x, y et z) et t est le temps78
97Le graphe suivant illustre une des solutions à l’équation (exemple 21).
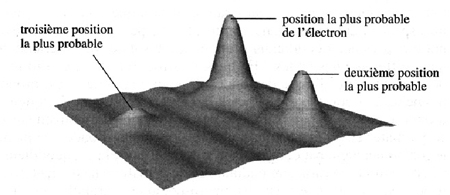
Exemple 21. Probabilités de position d’un électron79.
98Cette interprétation probabiliste plutôt que déterministe provient de la nature totalement statistique du monde quantique : il est impossible de prédire avec exactitude la position d’un électron, qui n’orbite pas de manière newtonienne mais qui se situe « plus ou moins là », mais de manière aléatoire. Les orbitales atomiques sont des ondes de probabilité et non pas des couches d’orbites physiques. L’état de la matière à l’échelle quantique n’est plus univoque, noir ou blanc, mais présente des dégradés de « couleurs » plus ou moins probables. Plus la couleur est claire, plus cette position est probable (exemple 22).
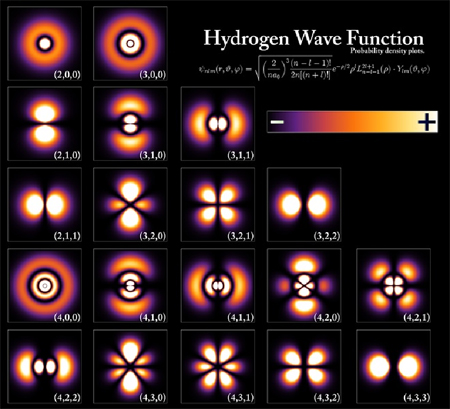
Exemple 22. Orbitales de l’atome d’hydrogène80.
99Par exemple, on fixe à 95 %81 la probabilité d’un électron d’être dans telle orbitale, en fonction de son énergie, mais pas à 100 %. Il peut momentanément être tout à fait ailleurs. Ainsi, « l’effet tunnel » permet à des particules de traverser des obstacles avec un faible pourcentage de probabilité mais pas nul, ce que la physique classique déterministe ne permet pas du tout ; cet effet est désormais utilisé quotidiennement (transistors, diodes, microscopes…)82.
100Cette nature irréductiblement statistique et aléatoire pose de nombreux problèmes, au niveau microscopique, à la causalité et à la continuité spatio-temporelle. Ainsi, si à un instant donné une particule se trouve plus ou moins ici, on ne peut pas simplement dire qu’elle était juste à côté un instant auparavant. Cela dit, si on la détecte, les mathématiques se retrouvent profondément modifiées. La mesure provoque une « réduction » du paquet d’ondes de Schrödinger (exemple 23).
101Ici, la particule n’est bien détectée qu’à un seul endroit. Simplement, lors de la mesure suivante, la particule sera ailleurs, probablement près d’un autre pic de la courbe de gauche. La particule ne suit pas une trajectoire définie, mais la détection effectue un tirage de probabilité parfaitement aléatoire.

Exemple 23. « Réduction » de l’onde de probabilité par la mesure83.
102Cette théorie choqua énormément Einstein (« Le Vieux ne joue pas aux dés ! » aurait-il écrit à Born)84, qui s’opposa à la théorie quantique tant qu’il le put85, bien que ce soient ses travaux sur la lumière qui aient fondé cette approche et qui lui valurent le prix Nobel. Il faut aussi ajouter que l’interprétation sur la nature exacte de cette réduction fait l’objet de débats, voir le paragraphe 6.9. Elle pourrait n’être qu’un épiphénomène mathématique86.
103Concrètement, les équations quantiques sont complexes et offrent peu de solutions analytiques détaillées : l’oscillateur harmonique, la particule dans une boîte et l’ion hydrogène. Même l’atome d’hélium est en réalité trop complexe pour une description exhaustive. Le reste est approximé par des théories perturbatives de bonne qualité. Différentes formulations mathématiques sont employées : matrices d’Heisenberg, ondes de Schrödinger, fonctions de Dirac, intégrale de chemins de Feynman, espaces d’Hilbert, chacune ayant des applications privilégiées.
De nombreuses incertitudes (1927)
104Les mathématiques et les expériences quantiques sont intraitables à un autre niveau essentiel : il est totalement impossible de connaître simultanément et avec précision la position q et la quantité de mouvement p d’une particule quantique. Heisenberg formalise ce principe d’incertitude (1927, exemple 24) :
105∆q ∆p ≈ h / 2*2π
Exemple 24. Relation d’incertitude.
106Où h est la constante de Planck87. On écrit aussi (exemple 25).
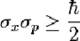
Exemple 25. Autre formulation du principe d’incertitude.
107Où x est la déviation standard de la position, p la déviations standard de la quantité de mouvement et ħ la constante de Planck divisée par 2π.
108Pourquoi ? Cela n’est pas dû à des difficultés expérimentales. La nature statistique de l’univers quantique implique une incertitude essentielle, constitutive de toute chose. De plus (ce n’est pas la cause), l’acte d’observer un phénomène le modifie : les photons à haute énergie nécessaires pour « regarder » une particule atomique interfèrent avec elle de manière importante. L’apport énergétique est tel que le mouvement ou la position de la particule s’en trouvent modifié.
109Une autre formulation, plus musicale sans doute, se fait en termes d’énergie, de temps et de fréquence.
110Ainsi, à partir de l’équation liant l’énergie et la fréquence (exemple 26).

Exemple 26. Énergie et pulsation.
111Où est la fréquence en Hz fois 2π,
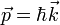 et celle liant la quantité de mouvement d’un photon et sa longueur d’onde (exemple 27).
et celle liant la quantité de mouvement d’un photon et sa longueur d’onde (exemple 27).
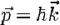
Exemple 27. Quantité de mouvement d’un photon.
112Où k = 2π/ longueur d’onde 88, on peut obtenir la longueur d’onde de Broglie (exemple 28).
113 = h/p89
Exemple 28. Longueur d’onde de Broglie.
114Et une nouvelle expression de l’incertitude d’Heisenberg (exemple 29).
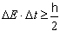
Exemple 29. 3e formulation du principe d’incertitude.
115La variation (étalement) de l’énergie E est donc aussi un étalement fréquentiel (∆ k) tandis qu’il y a aussi un étalement temporel ∆t ou de position ∆x. On peut représenter la chose graphiquement (exemple 30).
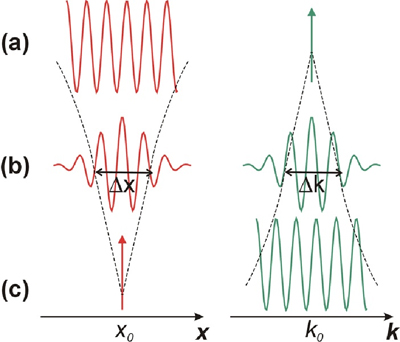
Exemple 30. Incertitudes.
« Vues spatiale (position) et fréquentielle (impulsion) de (a) une onde, (b) un paquet d’onde et (c) un corpuscule. L’onde étant de fréquence pure, son impulsion est définie, mais elle n’est pas localisée dans l’espace. Inversement, le corpuscule est localisé, mais n’a pas de fréquence déterminée. Le cas général est celui du paquet d’onde qui est distribué en fréquence comme en espace. Du fait de la dualité entre les deux représentations l’étalement spatial est inversement proportionnel à l’étalement fréquentiel »90.
116De nombreuses conséquences, philosophiques autant que scientifiques en découlent91. Principalement, la parfaite certitude classique doit laisser place à un flou relatif tandis que l’acte d’observation ne peut plus être neutre : l’observateur bouleverse le phénomène observé, cela sera approfondi infra. Cette incertitude fondamentale constitue la principale différence entre le monde microscopique de l’atome et le monde méso et macroscopique qui nous est familier.
Espace quantique
117En conséquence, la nature fondamentale de l’espace lui-même s’en trouve modifiée. Au niveau le plus fin, le vide, la trame spatiale devient sujette à l’incertitude ; elle-même se trouve être fluctuante et discontinue, elle est une véritable « mousse » quantique, pleine de soubresauts et trous (exemple 31)92.

Exemple 31. Mousse quantique93.
118Cela pose un grave problème à la théorie de la relativité qui demande un espace lisse et continu. En topologie, la discontinuité et les trous ont un impact majeur sur les calculs.
119Y a-t-il aussi incertitude temporelle ? Nous avons déjà vu que oui : le ∆t de l’exemple 29.
Ondes matérielles
120La matière et le temps ne sortent pas indemnes de ces perspectives quantiques :
1211. Comme la lumière, la matière (électrons, nucléons…) possède une double nature corpusculaire et ondulatoire : les ondes associées de Broglie (1923). Dans certain cas, la matière se comporte comme un corps dans d’autres cas, elle se comporte comme une onde.
1222. Une onde de quoi ? Une onde de probabilité quantique (fonction d’onde de Schrödinger) une fois encore.
1233. Les ondes matérielles ont bien été démontrées par expériences de diffractions d’électrons, de protons et d’ions.
Doubles fentes et chemins de Feynman (1948)
124Des polémiques et des expériences ont mis en valeur le fameux « paradoxe » de la double fente quantique, troublant quant à ses implications sur le temps. Si l’on bombarde une cible à travers une fente avec une série de particules ou de photons, ceux-ci se distribuent autour de cette fente. S’il y a deux fentes, la théorie classique laisse supposer deux distributions côte à côte (exemple 32 et 33a). Pourtant, lorsqu’on bombarde un écran cible d’électrons, à travers une double fente de largeur adaptée, on retrouve un motif d’interférences plutôt caractéristique des ondes. Les chercheurs estiment que ce sont les ondes associées aux électrons qui interfèrent (exemple 33b). Oui, des ondes de probabilité interfèrent matériellement avec des fentes physiques.

Exemple 32. Distribution et interférences.
125Le pic de gauche représente une intensité lumineuse plus importante lorsque beaucoup d’électrons touchent la cible tandis que les croisements d’ondes de droite créent une série de pics lumineux et de creux sombres (exemple 33).

Exemple 33. Double distribution et interférences94.
126Le plus troublant est que des interférences se produisent même s’il n’y a qu’une particule qui passe les fentes à la fois. Dans la figure suivante (exemple 34), une seule particule à la fois sort du canon à électron et traverse les fentes. Pourtant, une à une, ces particules reconstituent le motif d’interférence ondulatoire caractéristique (exemple 34c) :
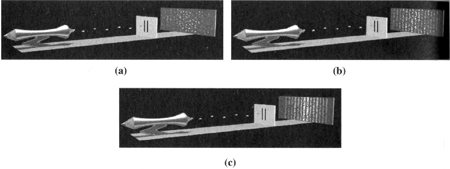
Exemple 34. Dualité onde-matière95.
127Ce résultat paradoxal implique que les particules se comportent comme des ondes même si elles circulent une à la fois. Il n’y a pas dans ce cas plusieurs électrons qui interagissent. Dans ce cas, comment les particules « savent-elles » où aller pour créer ce motif d’interférence ?
128Une variante de ce test est encore plus troublante. On a vu, exemple 23, que la détection d’une particule provoque une réduction des différents pics de probabilité à une seule position physique précise. Si on dédouble le dispositif précédent, en incluant un émetteur de particules particulières (dites intriquées) et un détecteur permettant de savoir par laquelle des fentes96 la particule est passée, le motif d’interférence disparaît complètement pour faire place à la double distribution de l’exemple 32. Plus paradoxal encore, si la particule est bien détectée dans l’une ou l’autre fente mais que le résultat de cette mesure est effacé avant que la particule n’atteigne la cible, le motif d’interférence revient97 !
129En fait, on ignore absolument ce que font les particules entre le canon, les fentes et les écrans de mesures. Selon Richard Feynman, on peut calculer qu’elles empruntent tous les chemins possibles (fente a, fente b, fentes a et b…) dans un état virtuel qui ne s’actualise et ne se condense qu’au moment de la mesure (exemple 35).
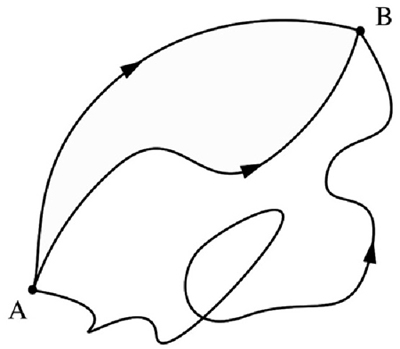
Exemple 35. Trois trajectoires de A à B. Chacune (et toutes les autres) contribuent à l’intégrale de chemin de Feynman98.
130Feynman a montré qu’il faut tenir compte de toutes les trajectoires possibles pour effectuer un calcul de la surface balayée par celles-ci (intégration), Cela est fort troublant pour le sens commun et pour le scientifique. Non seulement la matière se comporte tantôt comme une particule tantôt comme une onde, mais on retrouve ici un phénomène très paradoxal. Y a-t-il communication instantanée entre les particules intriquées, violant ainsi la vitesse lumière comme limite absolue ? Communiquent-t-elles indépendamment du temps ?
131Selon Alain Aspect, auteur principal de l’expérience d’Orsay, après les travaux théoriques de John Bell99, les particules intriquées ne communiquent pas instantanément,mais constituent plutôt un système unique et cohérent, en pratique une seule particule composite, peu importe la distance entre ses particules constitutives. On a réalisé au CERN une variante de l’expérience où les particules étaient séparées de plusieurs kilomètres, ce qui est une distance infinie à l’échelle microscopique, tout en maintenant leur intrication. Certains optimistes imaginent employer des particules intriquées pour communiquer plus vite que la lumière ou même voyager dans le temps, dans un certain sens100.
132Plusieurs phénomènes quantiques génèrent de telles particules intriquées et des groupes cohérents de particules101. Pourtant, on ne peut jamais observer la chose à notre échelle macroscopique. Les lois quantiques ne s’appliquent qu’aux objets réellement minuscules (pas même aux virus102). Bon nombre des chercheurs estiment que cette décohérence se produit à nos échelles à cause des multiples interactions des particules du monde réel avec ce dernier, provoquant très vite des « réductions » quantiques et un comportement familier103. C’est la théorie de la décohérence.
Le chat de Schrödinger et interprétations de la mécanique quantique
I don’t like it, and I’m sorry I ever had anything to do with it104
133Dans cette célèbre expérience de pensée, un chat dans une boîte fermée sera empoisonné ou non, en fonction du déclenchement aléatoire d’une réaction nucléaire. Cette réaction implique les probabilités quantiques. Les calculs les plus précis laissent penser que tant que l’on n’ouvre pas la boîte, l’état du chat est indéterminé (ni vivant, ni mort). L’acte d’ouvrir « réduit » les ondes de probabilités quantiques et une seule solution se cristallise : dans x % des cas, le chat est retrouvé vivant et dans le reste des cas, il est mort. Est-ce que cela veut dire que le chat est vraiment mi-mort mi-vivant ? ! Schrödinger trouvait cela absurde pour sa part, comme l’indique l’exergue.
134Ce comportement troublant a pourtant été approché expérimentalement105. Dans un montage adapté, un groupe d’atomes émet de la lumière dans un certain pourcentage de temps et reste sombre le reste du temps, précisément en fonction des équations quantiques. On peut réussir la démonstration en isolant un seul atome et en mesurant avec finesse ses émissions lumineuses. Même seul, il brille par moments et reste sombre par moments, basculant de façon totalement aléatoire d’un état à l’autre. La superposition théorique des états sombres et lumineux s’incarne ici en une fluctuation aléatoire entre les deux états. Doit-on en déduire que le chat de Schrödinger est vivant jusqu’à ce qu’une fluctuation aléatoire déclenche le mécanisme mortel ? Ressuscite-t-il ensuite ? Sans doute pas. Il y a en fait dans ce dispositif un laser de sonde, qui interagit avec le système et provoque en permanence la réduction des probabilités. Cela démontre tout de même la nature parfaitement aléatoire de ces réductions plutôt qu’un déterminisme clair.
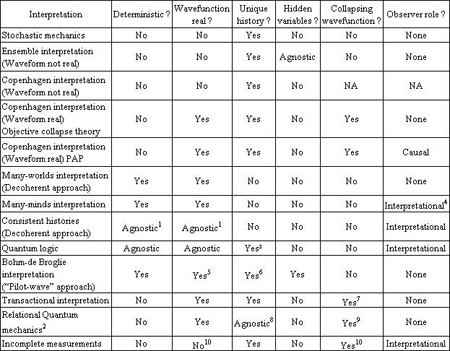
1 If wavefunction is real then this becomes the many-worlds interpretation. If wavefunction less than real, but more than just information, then Zurek calls this the “existential interpretation”.
2 Quantum mechanics is regarded as a way of predicting observations, or a theory of measurement.
3 But quantum logic is more limited in applicability than Coherent Histories.
4 Observers separate the universal wavefunction into orthogonal sets of experiences.
5 Both particle AND guiding wavefunction are real.
6 Unique particle history, but multiple wave histories.
7 In the TI the collapse of the state vector is interpreted as the completion of the transaction between emitter and absorber.
8 Comparing histories between systems in this interpretation has no well-defined meaning.
9 Any physical interaction is treated as a collapse event relative to the systems involved, not just macroscopic or conscious observers.
10 The nature and collapse of the wave function are derived, not axiomatic.
Exemple 36. Caractéristiques des interprétations quantiques106.
135L’interprétation de ces paradoxes ouvre la porte à de nombreuses théories peu quotidiennes107 : Einstein et ses proches croyaient qu’il y avait des variables cachés encore à découvrir, pour certains (Hawking, Feynman), chaque alternative dans ces situations ambiguës génère des mondes parallèles, d’autres (Wheeler) estiment qu’il y a interaction entre l’intelligence humaine et le dispositif expérimental, tandis que d’autres encore (Ghirardi, Penrose) croient que l’effondrement de la fonction d’onde est lui aussi aléatoire et indépendant de l’acte de mesure ou d’autres privilégient la piste de la décohérence évoquée ci-dessus. Le tableau suivant donne un bon résumé des multiples interprétations (exemple 36).
136L’interprétation dominante de ces différents paradoxes, dite « interprétation de Copenhague », lieu de résidence de Niels Bohr, invite à abandonner le « réalisme », sens commun issu des phénomènes aux échelles méso et macroscopique, et à pratiquer plutôt un certain détachement. Cela entraîne à accepter l’existence de la nature probabiliste plutôt que déterministe de l’échelle quantique, la dualité onde-matière et insiste sur le fait qu’avant les mesures, la question de savoir où se trouve telle particule n’a tout simplement pas de sens. Il faut cependant ajouter que la théorie des mondes multiples est aussi très bien reçue108, de même que celle de la décohérence, plus récente et confirmée par un nombre important d’expériences109.
137Quelle que soit l’interprétation, cela marche très bien : tous les travaux atomiques et nucléaires depuis 80 ans ont confirmé la pertinence et la précision de la théorie, au point où certains demandent aux autres de se « taire et de calculer », c’est-à-dire, de ne pas trop se focaliser sur des interprétations polémiques et d’agir de façon pragmatique110. Accélérateurs de particules, mais aussi ordinateurs, lasers, microscope à effet tunnel (à base d’incertitude), et mille autre choses le prouvent quotidiennement, la mécanique quantique correspond bien aux données réelles. Certaines prédictions théoriques atteignent les 10 décimales de précisions, ce qui est un tour de force impressionnant.
Un temps quantifié ?
138Après avoir quantifié l’énergie, différentes théories proposent aussi de quantifier le temps et/ou l’espace. En ce qui concerne le temps, on retrouve deux candidats au statut de quantum temporel :
1391. le temps de Planck (~ 5,4 x 10-44s).
1402. Le chronon de Caldirola (6.97 x10-24 s).
141Le premier temps est tellement infinitésimal que l’on doute de ne jamais y parvenir. Le second semble plus près de l’expérimental, sachant que l’on atteint aujourd’hui l’ordre de l’attoseconde (0,000000000000000001s)111. Le chronon n’est pas encore démontré, mais il contribue aux théories non-cordistes de la gravité quantique, par exemple la théorie de la gravitation quantique à boucles112. Cette théorie est intéressante car elle propose une géométrisation significative de la gravité, des champs électriques, magnétiques, de l’espace et un temps quantifié. Il faut cependant ajouter que ces théories ne sont pas encore très abouties ni guère acceptées par la communauté113 car elles ne prédisent encore rien de nouveau.
142Pourtant, cette idée ne choque guère le musicien occidental utilisant du temps quantifié (les figures rythmiques) depuis le XIIIe siècle. Une pensée musicale additive, comme celle de la musique indienne ou celles de Stockhausen ou Glass, vient immédiatement à l’esprit.
Vers une conception du temps réellement contemporaine
Incompatibilités
143Les deux théories majeures de la physique contemporaine sont remarquablement exactes, prolifiques et confirmées par l’expérience. Elles sont toutefois incompatibles entre elles. Comme on l’a vu, la première postule un espace-temps continu et relatif aux vitesses/masses et une physique déterministe. La seconde utilise un temps linéaire constant (non-relativiste) et un espace foncièrement aléatoire. La causalité classique s’y voit remplacée par les statistiques indéterminées et une incertitude constitutive.
144La combinaison de ces deux physiques est nécessaire pour comprendre le Big Bang ou les trous noirs, c’est-à-dire l’univers et son devenir, mais encore les tout petits systèmes. Cela devient aussi critique lorsque la taille des microcircuits atteint sa limite et que les phénomènes quantiques ne sont plus négligeables.
145Cela dit, après quelques années très optimistes, la prudence demeure de mise :
« Observed physical phenomena in the early 21st century can be described well by quantum mechanics or general relativity, without needing both. This can be thought of as due to an extreme separation of scales at which they are important. Quantum effects are usually important only for the “very small”, that is, objects no larger than ordinary molecules (for instance as of 2009 even viruses have not been observed to undergo double-slit diffraction). General relativistic effects, on the other hand, show up only for the “very large” bodies such as collapsed stars. (Planets’ gravitational fields, as of 2009, are well-described by linearized gravity, so strong-field effects, any effects of gravity beyond lowest nonvanishing order in phi/c2, have not been observed even in the gravitational fields of planets and main sequence stars.) Classical physics seems to be adequate over an enormous range of masses of objects from about 10-23 to 1030 kg. Thus there is a want of experimental evidence relating to quantum gravity, but the “gap” spans 53 orders of magnitude »114.
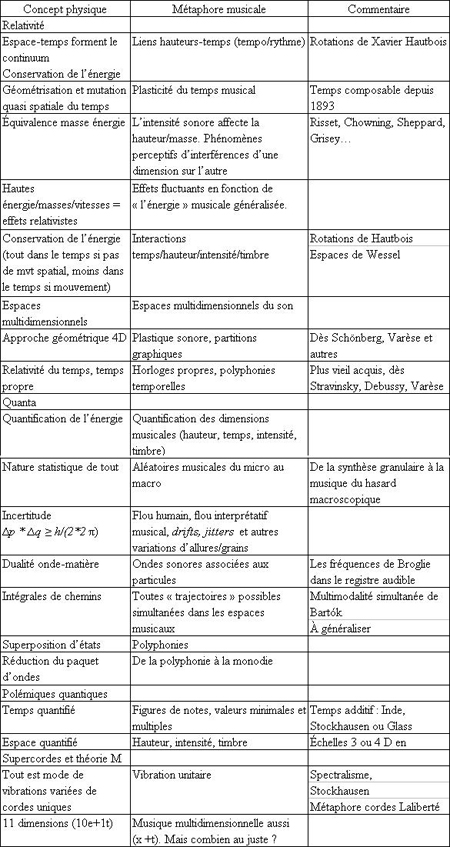
Exemple 37. Quelques métaphores.
Quelques pistes plus fraîches
146Ces préalables à un travail musical se terminent sur cette note de scepticisme utile. J’aurais souhaité aborder à ce point d’autres questions, moins bien balisées, par exemple quelles sont les conceptions du temps implicites dans les théories encore sujettes à polémiques ou n’ayant pas encore reçu de confirmations expérimentales ? Plus spécifiquement, quelles sont les incidences des hypothèses suivantes :
1471. Supercordes, théorie des branes et théorie M115.
1482. Autres théories quantiques supersymétriques116.
1493. Hypothèse d’une vitesse variable de la lumière117.
1504. Temps et espace quantifiés et gravitation quantique à boucles118.
151Je ne puis pour le moment qu’inviter à consulter les références et à lire une prochaine publication sur cette question.
152Pour commencer à relier tout cela à la musique, voici quelques métaphores fécondes sur lesquelles je souhaite encore travailler. Que l’on en excuse la formulation lapidaire ou peu aboutie (exemple 37).
Conclusion
153Cent ans après les révolutions contemporaines de la physique, le temps semble mûr pour sonder leurs incidences sur la pensée musicale réelle ou métaphorique. Cet article tente d’en poser des préalables synthétiques, avant de pouvoir procéder à une application musicale concrète. Je voulais aussi amorcer des débats autour de ces questions de grande importance, si l’on souhaite que le paysage mental du compositeur soit réellement contemporain de sa culture scientifique et technique.
Notes
1 Étant compositeur plutôt que physicien, je m’adresse ici au lecteur musicien. Les physiciens auront accès à des travaux plus spécifiques et complets. J’invite surtout à l’instauration d’un dialogue sur les questions abordées.
2 « Calendrier », infr.wikipedia.org, consulté en juin 2009. Wikipedia, en dépit des nombreuses réserves que l’on peut apporter, est une source fascinante pour le sujet traité ici. La communauté physique s’en sert abondamment et les articles sont assez fiables, pour peu que l’on pratique le recoupement d’informations. La comparaison des versions en langues différentes est souvent très utile.
3 Le délicieux Gödel, Escher, Bach, les brins d’une guirlande éternelle, développe abondamment sur ce paradoxe, Douglas Hofstadter, Gödel, Escher, Bach, les brins d’une guirlande éternelle, traduction de Jacqueline Henry et Robert French Paris, IntrerEditions, 1979 (1985 pour la traduction française), 884 p.
4 Étienne Klein, Les tactiques de Chronos, Paris, Flammarion, coll. « Champs », 2004, 220 p. Pour l’opposition des formes et une lecture critique, consultez en particulier les pp 73-92.
5 Paul Klee, Cours du Bauhaus, Weimar 1921-22, contributions à la théorie de la forme picturale, traduction de Claude Riehl, Paris, Hazan, 2004, 224 p.
6 Voir aussi James Gleick Faster, the acceleration of just about everything, New York, Vintage Books, 1999, 324 p, ainsi qu’« Heures_canoniales », « Calendrier_maya » ou « Dionysius_Exiguus », in fr.wikipedia.org, consultés en juin 2009.
7 Étienne Klein, op. cit., p. 112.
8 Cité dans Klein, op. cit., p. 86.
9 Et malgré le fait que dans le calcul intégral et différentiel, on utilise « l’instant », la tranche de temps infinitésimal.
10 Pour une version contemporaine de cette idée (la symétrie T) voir « Time_reversal_operator », inen.wikipedia.org, consulté en juillet 2009.
11 Les affinités électives de Goethe, par exemple.
12 Voir la citation du chapitre « Vers une conception du temps réellement contemporaine ».
13 Newton les évoque lui-même.
14 Un film silencieux passé à l’envers, lorsque les images sont judicieusement choisies, ne semble pas absurde.
15 Il se solutionne toutefois par approximation (théorie des perturbations). Voir « Problème_à_Ncorps » et « Henri_Poincaré », in fr.wikipedia.org, consultés en juin 2009.
16 La science de l’électricité, des ondes, des champs et du magnétisme formulée par James Clerk Maxwell en 1861.
17 Sans parler des inventions techniques de la fin du XVIIIe siècle, comme la machine à vapeur de Papin/Watt.
18 Les formalismes usuels sont utilisés ici, pas ceux des premiers auteurs.
19 La réalité est souvent plus complexe, de nombreux cas d’éloignement de l’équilibre tiède existent, comme le prouve notre monde quotidien.
20 Étienne Klein, op. cit. pp. 125-135.
21 Par exemple celle de l’exemple 9.
22 Brian Greene, La magie du cosmos, traduction de Céline Laroche, Paris, Robert Laffont, 2004, pp 197-200.
23 Voir le chapitre « Expansion et destin de l’univers ».
24 Voir « Ludwig_Boltzmann », inen.wikipedia.org, consulté en juillet 2009. Il était atomiste et statisticien, ce qui n’était pas encore apprécié.
25 Où k est la constante de Boltzmann et le nombre des états d’énergie équiprobables possibles du système. On l’écrit aussi : S = k loge W
26 Voir « Expérience_de_Michelson-Morley », infr.wikipedia.org, consulté en juillet 2009.
27 Voir le chapitre « Nature duale de la lumière (1905) ».
28 En fait, l’équation complète est E2 = p2c2 = m2c4, où p est la quantité de mouvement et m la masse.Cela implique l’existence d’énergies négatives, les anti-particules symétriques des particules ordinaires, comme le comprendra Dirac.
29 Plus simplement on peut écrire s2 = c2 Δt2 - Δr2 où s est l’intervalle spatiotemporel, t le temps et r la position dans les trois dimensions d’espace x, y et z.
30 D’après Brian Greene, L’univers élégant, traduction de Céline Laroche, Paris, Robert Laffont, 1999, p. 67.
31 Depuis, on a aussi démontré que l’électromagnétisme de Maxwell ne fonctionne qu’avec trois dimensions d’espace et un e de temps. « Spacetime », in en.wikipedia.org, consulté en juillet 2009.
32 Cet « espace de Minkowski » est une « variété » à quatre dimensions. Les mathématiciens (Gauss, Hamilton…) travaillaient sur des objets multidimensionnels depuis le milieu du XIXe siècle.
33 Brian Greene, La magie du cosmos, op. cit., pp. 162-177.
34 Ibid., p. 84.
35 Il manque une dimension spatiale, la profondeur z.
36 L’espace-temps d’Einstein s’appréhende de façon géométrique.
37 Ibid., p. 169.
38 D’après « General_Relativity », in en.wikipedia.org, consulté en juillet 2009.
39 Pour des discussions plus avancées, voir par exemple Stephen Hawking et Roger Penrose, La nature de l’espace et du temps, traduction de Françoise Balibar, Paris, Gallimard, coll. « Folio, essais », 1997, 215 p, ou Brian Greene, L’univers élégant, op. cit., pp. 255-308.
40 Ou plus. Par exemple la théorie actuelle (« branaire ») des supercordes implique 10 dimensions d’espace et 1 de temps.
41 Par contre, en tant que continuum, l’espace-temps demeure un absolu. Voir Brian Greene, La magie du cosmos, op. cit., p. 85.
42 Il affirme avant Einstein, dans La machine à explorer le temps, que le temps est une dimension spatiale.
43 Mais pas l’espace pris indépendamment du temps. Celui-ci demeure quasi-euclidien, comme on peut l’observer au quotidien.
44 Voir le chapitre « Expansion et destin de l’univers ».
45 E égale toujours mc2. Voir « Équation_d’Eintein », in fr.wikipedia.org, consulté en juillet 2009.
46 D’après Brian Greene L’univers élégant, op. cit. pp. 90-93. Il présente aussi une version animée de cela dans cette conférence : http://www.youtube.com/watch ?v =YtdE662eY_M, consulté en juillet 2009.
47 Loin des visions extrêmes de science-fiction à la Lovecraft, les géométries non-euclidiennes décrivent des espaces courbes désormais bien compris.
48 Par exemple, les vols longs courriers empruntent des trajets proches des géodésiques pour minimiser les distances parcourues, comme on peut le voir dans la plupart des brochures de bord.
49 D’après « Relativité_générale », in fr.wikipedia.org, consulté en juillet 2009.
50 John R. R. Tolkien, The Silmarillon, Londres, Harper Collins, 1977, pp. 338-339.
51 Brian Greene L’univers élégant, op. cit., pp. 289-292.
52 « Gravity_Probe_B », in en.wikipedia.org, consulté en juin 2009. La courbure du temps (frame dragging) se révèle toutefois moins importante que celle de l’espace.
53 « Relativité_générale », loc. cit., consulté en juillet 2009.
54 « time », in en.wikipedia.org, consulté en février 2009.
55 « Gravitational_time_dilatation », in en.wikipedia.org, consulté en juillet 2009.
56 À peu près 8987551787400000 m2/s2.
57 On se demande comment construire un appareil de ce type !
58 Ou sa compression, à vrai dire. En effet, le sens du mouvement est une fois encore symétrique. L’univers peut soit se dilater soit se comprimer comme on le verra infra.
59 En simplifiant plusieurs paramètres, on peut obtenir une proportionnalité directe Gµ =8Tµ.
60 « Big_bang », in fr.wikipedia.org, consulté en juillet 2009.
61 « inflaton », in fr.wikipedia.org, consulté en juillet 2009.
62 Brian Greene, La magie du cosmos, op. cit., pp. 354-364.
63 Lemaître parlait plutôt de sa « théorie de l’atome primitif ».
64 « Georges_Lemaître »,in fr.wikipedia.org, consulté en juin 2009.
65 « Big_bang », in fr.wikipedia.org, consulté en juillet 2009.
66 D’après « Big_bang », in en.wikipedia.org, consulté le 18 juin 2009. L’expérience WMAP est la mesure par radiotélescope du résidu de l’émission de photos 400 000 après le big-bang (tache verte sur la gauche).
67 « Ultimate_fate_of_the_universe », in en.wikipedia.org, consulté en juillet 2009.
68 À moins que la dilatation maximale entraîne un déchirement (big rip) de l’univers.
69 On songe ici au Conter-clock world de Philip K. Dick, Berkeley Books, 1967, 160 p.
70 Les cycles cosmiques de Brahmâ.
71 « Graphical_timeline_from_Big_Bang_to_Heat_Death », in en.wikipedia.org, consulté en juillet 2009.
72 La science n’échappe pas à la plupart des phénomènes culturels humains et a une histoire polémique et relativement peu linéaire, comme nous l’enseigne l’épistémologie.
73 « Trinity_test », in en.wikipedia.org, consulté en juillet 2009.
74 Fritjof Capra, Le tao de la physique, Paris, Sand, 2/1975 (1985 pour la traduction française), 355 p.
75 Les échelles microscopiques impliquent plutôt la théorie quantique.
76 « Light », in en.wikipedia.org, consulté en juillet 2009.
77 Alain Aspect et al., Demain la physique, Paris, Odile Jacob, 2004, p. 132.
78 L’équation de Schrödinger est variable dans l’espace et le temps, mais on simplifie souvent cet aspect.
79 D’après Brian Greene, La magie du cosmos, op cit., p. 117.
80 « Quantum_state », in en.wikipedia.org, consulté en juin 2009.
81 « Orbitale_atomique », in fr.wikipedia.org, consulté en juillet 2009. On distingue ainsi « l’orbite » à trajectoire définie de « l’orbitale atomique » de nature probabiliste.
82 « Effet_tunnel », in fr.wikipedia.org, consulté en juillet 2009
83 D’après Brian Greene, La magie du cosmos, op. cit., p. 151.
84 Voir la note 42 de « Max_Born », in en.wikipedia.org, consulté en juillet 2009.
85 Par exemple avec le célèbre paradoxe EPR. « Paradoxe_EPR », in en.wikipedia.org, consulté en juillet 2009.
86 « Wavefunction_collapse », in en.wikipedia.org, consulté en juillet 2009.
87 6,626075 * 10-34 J s
88 = vitesse de l’onde/fréquence. Voir Horst Stöcker et al., Toute la physique, traduction de Francis Jundt et Georges Guillaume, Paris, Dunod, 1999, pp. 826-836.
89 La longueur d’onde de Louis de Broglie permet de calculer les ondes « matérielles » associées aux particules.
90 « incertitude », in fr.wikipedia.org, consulté en juillet 2009.
91 Voir Werner Heisenberg, La partie et le tout, Paris, Flammarion, coll. « champs », 1969 (1972 pour la traduction française), 338 p.
92 « quantum_foam », in en.wikipedia.org, consulté en juillet 2009.
93 « quantum foam », in universe-review.ca, consulté en juillet 2009.
94 D’après Brian Greene, La magie du cosmos, op. cit., p. 113.
95 Ibid., p. 114.
96 En réalité, il y a des modifications : il s’agit cette fois de séparateurs, de détecteurs intermédiaires de spin et d’écran final. Le résultat est analogue à ce qui est décrit, cependant. Brian Green, la magie du cosmos, op. cit., donne un schéma p. 230.
97 Voir Alain Aspect et al., op. cit., pp 139-146, et Brian Greene, La magie du cosmos, op. cit., pp. 134-156 et pp. 218-263.
98 « Intégrale_de_chemin », in fr.wikipedia.org, consulté en juillet 2009. Il est à remarquer que cette formulation mathématique utile n’est pas forcément réelle. Feynman lui-même ne croyait pas à la réalité de cet outil pratique.
99 Einstien et ses collègues opposés à la physique quantique trouvaient cela absurde et se servaient de cette théorie pour invalider la physique quantique. Bell, Aspect et les autres expérimentateurs leur ont donné tort.
100 « time_travel », in en.wikipedia.org, consulté en juin 2009.
101 « Condensat_de_Bose-Einstein », in fr.wikipedia.org, consulté en juillet 2009.
102 « Quantum_gravity », in en.wikipedia.org, consulté en juin 2009.
103 Alain Aspect et al., op. cit., pp 154-156.
104 Erwin Schrôdinger, cité par John Gribbin, In search of Schrödinger’s cat, Quantum physics and reality, Londres, Black Swan, 1984, 302 p.
105 Alain Aspect et al., op. cit., pp. 147-157.
106 « Interpretation_of_quantum_mechanics », in en.wikipedia.org, consulté en juillet 2009.
107 Ibid.
108 Michael Clive Price, « Q1 Who believes in many-worlds », in hedweb.com/everett, consulté en juillet 2009.
109 « decoherence_quantique », in fr.wikipedia.org, consulté en juin 2009.
110 Voir Hawking et Penrose, op. cit., pp 39-40.
111 « Femtoseconde », in fr.wikipedia.org, consulté en juin 2009.
112 « Chronon » et « Loop_quantum_gravity », in en.wikipedia.org, consulté en juin 2009.
113 Lee Smolin, Rien ne va plus en physique, traduction de Alexeï Grinbaum, Paris, Dunod, coll. « Quai des sciences », 2006, 488 p.
114 « Quantum gravity » loc. cit.
115 Voir Martin Laliberté, « Les “supercordes”, une nouvelle métaphore musicale ? »,in M. Solomos (éd.) La métaphore lumineuse : Gérard Grisey et Iannis Xenakis, Paris, l’Harmattan, 2003, pp. 123-146.
116 Brian Greene, L’univers élégant, op. cit., pp. 196-207 et Alain Aspect et al., op. cit., pp. 87-109.
117 João Maguejio, Plus vite que la lumière, Paris, Dunod, coll. « Quai des sciences », 2003, 323 p.
118 Lee Smolin, op. cit.
Citation
Auteur
Quelques mots à propos de : Martin Laliberté








